ref：oracle 9i、10g編程藝術(shù)。
sqlplus允許建立一個(gè)login.sql，通過設(shè)置環(huán)境變量SQLPATH，指向文件所在目錄，每次啟動(dòng)sqlplus都會(huì)執(zhí)行這個(gè)腳本。
login.sql例子：

define _editor=notepad

set serveroutput on size 1000000

set trimspool on

set long 5000

set linesize 100

set pagesize 9999

column plan_plus_exp format a80

column global_name new_value gname

set termout off

define gname=idle

column global_name new_value gname

select lower(user) || '@' || substr( global_name, 1, decode( dot, 0,

length(global_name), dot-1) ) global_name

from (select global_name, instr(global_name,'.') dot from global_name );

set sqlprompt '&gname> '

set termout on

define _editor: sqlplus默認(rèn)的編輯器；
set serveroutput on size 1000000：默認(rèn)打開DBMS_OUTPUT,將緩沖區(qū)設(shè)置盡可能大；

posted @ 2009-03-16 22:07 donnie 閱讀(289) | 評(píng)論 (0) | 編輯收藏

How to grant select on system views like v$session to any user.

現(xiàn)象：
sys@ORCL> grant select on v$session to scott;
grant select on v$session to scott
*
第 1 行出現(xiàn)錯(cuò)誤:
ORA-02030: 只能從固定的表/視圖查詢

解決：
grant select on v_$session to scott;

posted @ 2009-03-16 21:59 donnie 閱讀(828) | 評(píng)論 (0) | 編輯收藏

flash player 9 安裝錯(cuò)誤：正在嘗試安裝的ADOBE FLASH PLAYER版本不是最新的。。。。

HKEY_LOCAL_MACHINE\SOFTWARE\Macromedia\FlashPlayer\SafeVersions]
將"9.0"，“10.0” 項(xiàng)刪除，重新安裝。

posted @ 2009-03-16 15:31 donnie 閱讀(2926) | 評(píng)論 (2) | 編輯收藏

CentOS

http://www.centospub.com/
CentOS 是 RHEL（Red Hat Enterprise Linux）源代碼再編譯的產(chǎn)物，而且在 RHEL 的基礎(chǔ)上修正了不少已知的 Bug ，相對(duì)于其他 Linux 發(fā)行版，其穩(wěn)定性值得信賴。

CentOS 4.4 的下載及安裝
http://www.centospub.com/make/install.html
從鏡像站點(diǎn)上下載ISO的鏡像文件

　　　　CD 1 : http://mirror.tini4u.net/centos/4.4/isos/i386/CentOS-4.4-i386-bin1of4.iso
　　　　CD 2 : http://mirror.tini4u.net/centos/4.4/isos/i386/CentOS-4.4-i386-bin2of4.iso
　　　　CD 3 : http://mirror.tini4u.net/centos/4.4/isos/i386/CentOS-4.4-i386-bin3of4.iso
　　　　CD 4 : http://mirror.tini4u.net/centos/4.4/isos/i386/CentOS-4.4-i386-bin4of4.iso
　　　　md5校驗(yàn)碼：http://mirror.tini4u.net/centos/4.4/isos/i386/md5sum

　　　　將上面所有文件（包括md5校驗(yàn)碼）下載到同一個(gè)目錄（文件夾）下。（這里，選擇了從CentOS的韓國(guó)鏡像站上下載。根據(jù)具體位置可以選擇距離近、速度快的景象站點(diǎn)。查找CentOS的鏡像請(qǐng)見官方鏡像站點(diǎn)列表。）

posted @ 2009-03-13 13:20 donnie 閱讀(108) | 評(píng)論 (1) | 編輯收藏

正態(tài)分布

http://wiki.mbalib.com/wiki/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83

正態(tài)分布

出自MBA智庫(kù)百科(http://wiki.mbalib.com/)

正態(tài)分布（normal distribution)

什么是正態(tài)分布

　　正態(tài)分布是一種概率分布。正態(tài)分布是具有兩個(gè)參數(shù)μ和σ2的連續(xù)型隨機(jī)變量的分布，第一參數(shù)μ是遵從正態(tài)分布的隨機(jī)變量的均值，第二個(gè)參數(shù)σ2是此隨機(jī)變量的方差，所以正態(tài)分布記作N(μ，σ2 )。遵從正態(tài)分布的隨機(jī)變量的概率規(guī)律為取 μ鄰近的值的概率大，而取離μ越遠(yuǎn)的值的概率越小；σ越小，分布越集中在μ附近，σ越大，分布越分散。正態(tài)分布的密度函數(shù)的特點(diǎn)是：關(guān)于μ對(duì)稱，在μ處達(dá)到最大值，在正（負(fù)）無(wú)窮遠(yuǎn)處取值為0，在μ±σ處有拐點(diǎn)。它的形狀是中間高兩邊低，圖像是一條位于x 軸上方的鐘形曲線。當(dāng)μ＝0，σ2 ＝1時(shí)，稱為標(biāo)準(zhǔn)正態(tài)分布，記為N（0，1）。μ維隨機(jī)向量具有類似的概率規(guī)律時(shí)，稱此隨機(jī)向量遵從多維正態(tài)分布。多元正態(tài)分布有很好的性質(zhì)，例如，多元正態(tài)分布的邊緣分布仍為正態(tài)分布，它經(jīng)任何線性變換得到的隨機(jī)向量仍為多維正態(tài)分布，特別它的線性組合為一元正態(tài)分布。

[編輯]

正態(tài)分布的發(fā)展

　　正態(tài)分布是最重要的一種概率分布。正態(tài)分布概念是由德國(guó)的數(shù)學(xué)家和天文學(xué)家Moivre于1733年受次提出的，但由于德國(guó)數(shù)學(xué)家Gauss率先將其應(yīng)用于天文學(xué)家研究，故正態(tài)分布又叫高斯分布高斯這項(xiàng)工作對(duì)后世的影響極大，他使正態(tài)分布同時(shí)有了“高斯分布”的名稱，后世之所以多將最小二乘法的發(fā)明權(quán)歸之于他，也是出于這一工作。高斯是一個(gè)偉大的數(shù)學(xué)家，重要的貢獻(xiàn)不勝枚舉。但現(xiàn)今德國(guó)10馬克的印有高斯頭像的鈔票，其上還印有正態(tài)分布的密度曲線。這傳達(dá)了一種想法：在高斯的一切科學(xué)貢獻(xiàn)中，其對(duì)人類文明影響最大者，就是這一項(xiàng)。在高斯剛作出這個(gè)發(fā)現(xiàn)之初，也許人們還只能從其理論的簡(jiǎn)化上來評(píng)價(jià)其優(yōu)越性，其全部影響還不能充分看出來。這要到20世紀(jì)正態(tài)小樣本理論充分發(fā)展起來以后。皮埃爾-西蒙·拉普拉斯很快得知高斯的工作，并馬上將其與他發(fā)現(xiàn)的中心極限定理聯(lián)系起來，為此，他在即將發(fā)表的一篇文章(發(fā)表于1810年）上加上了一點(diǎn)補(bǔ)充，指出如若誤差可看成許多量的疊加，根據(jù)他的中心極限定理，誤差理應(yīng)有高斯分布。這是歷史上第一次提到所謂“元誤差學(xué)說”——誤差是由大量的、由種種原因產(chǎn)生的元誤差疊加而成。后來到1837年，海根(G.Hagen)在一篇論文中正式提出了這個(gè)學(xué)說。

　　其實(shí)，他提出的形式有相當(dāng)大的局限性：海根把誤差設(shè)想成個(gè)數(shù)很多的、獨(dú)立同分布的“元誤差” 之和，每只取兩值，其概率都是1/2，由此出發(fā)，按狄莫佛的中心極限定理，立即就得出誤差(近似地)服從正態(tài)分布。皮埃爾-西蒙·拉普拉斯所指出的這一點(diǎn)有重大的意義，在于他給誤差的正態(tài)理論一個(gè)更自然合理、更令人信服的解釋。因?yàn)椋咚沟恼f法有一點(diǎn)循環(huán)論證的氣味：由于算術(shù)平均是優(yōu)良的，推出誤差必須服從正態(tài)分布；反過來，由后一結(jié)論又推出算術(shù)平均及最小二乘估計(jì)的優(yōu)良性，故必須認(rèn)定這二者之一(算術(shù)平均的優(yōu)良性，誤差的正態(tài)性) 為出發(fā)點(diǎn)。但算術(shù)平均到底并沒有自行成立的理由，以它作為理論中一個(gè)預(yù)設(shè)的出發(fā)點(diǎn)，終覺有其不足之處。拉普拉斯的理把這斷裂的一環(huán)連接起來，使之成為一個(gè)和諧的整體，實(shí)有著極重大的意義。

[編輯]

正態(tài)分布的主要特征

　　1、集中性：正態(tài)曲線的高峰位于正中央，即均數(shù)所在的位置。

　　2、對(duì)稱性：正態(tài)曲線以均數(shù)為中心，左右對(duì)稱，曲線兩端永遠(yuǎn)不與橫軸相交。

　　3、均勻變動(dòng)性：正態(tài)曲線由均數(shù)所在處開始，分別向左右兩側(cè)逐漸均勻下降。

　　4、正態(tài)分布有兩個(gè)參數(shù)，即均數(shù)μ和標(biāo)準(zhǔn)差σ，可記作N（μ，σ）：均數(shù)μ決定正態(tài)曲線的中心位置；標(biāo)準(zhǔn)差σ決定正態(tài)曲線的陡峭或扁平程度。σ越小，曲線越陡峭；σ越大，曲線越扁平。

　　5、u變換：為了便于描述和應(yīng)用，常將正態(tài)變量作數(shù)據(jù)轉(zhuǎn)換。

[編輯]

正態(tài)分布的應(yīng)用

　　1．估計(jì)正態(tài)分布資料的頻數(shù)分布

　　例1.某地1993年抽樣調(diào)查了100名18歲男大學(xué)生身高（cm），其均數(shù)=172.70cm，標(biāo)準(zhǔn)差s=4.01cm，①估計(jì)該地18歲男大學(xué)生身高在168cm以下者占該地18歲男大學(xué)生總數(shù)的百分?jǐn)?shù)；②分別求、、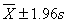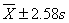范圍內(nèi)18歲男大學(xué)生占該地18歲男大學(xué)生總數(shù)的實(shí)際百分?jǐn)?shù)，并與理論百分?jǐn)?shù)比較。

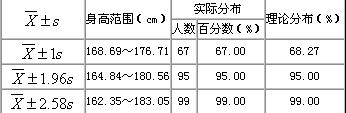
　　本例，μ、σ未知但樣本含量n較大，按式（3.1）用樣本均數(shù)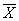和標(biāo)準(zhǔn)差S分別代替μ和σ，求得u值，u=(168-172.70)/4.01=-1.17。查附表標(biāo)準(zhǔn)正態(tài)曲線下的面積，在表的左側(cè)找到-1.1，表的上方找到0.07，兩者相交處為0.1210=12.10%。該地18歲男大學(xué)生身高在168cm以下者，約占總數(shù)12.10%。其它計(jì)算結(jié)果見表3.1。

　　表：1100名18歲男大學(xué)生身高的實(shí)際分布與理論分布

　　2．制定醫(yī)學(xué)參考值范圍：亦稱醫(yī)學(xué)正常值范圍。它是指所謂“正常人”的解剖、生理、生化等指標(biāo)的波動(dòng)范圍。制定正常值范圍時(shí)，首先要確定一批樣本含量足夠大的 “正常人”，所謂“正常人”不是指“健康人”，而是指排除了影響所研究指標(biāo)的疾病和有關(guān)因素的同質(zhì)人群；其次需根據(jù)研究目的和使用要求選定適當(dāng)?shù)陌俜纸缰担?0%，90%，95%和99%，常用95%；根據(jù)指標(biāo)的實(shí)際用途確定單側(cè)或雙側(cè)界值，如白細(xì)胞計(jì)數(shù)過高過低皆屬不正常須確定雙側(cè)界值，又如肝功中轉(zhuǎn)氨酶過高屬不正常須確定單側(cè)上界，肺活量過低屬不正常須確定單側(cè)下界。另外，還要根據(jù)資料的分布特點(diǎn)，選用恰當(dāng)?shù)挠?jì)算方法。常用方法有：

　　（1）正態(tài)分布法：適用于正態(tài)或近似正態(tài)分布的資料。

　　雙側(cè)界值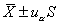：單側(cè)上界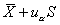：，或單側(cè)下界：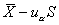

　　（2）對(duì)數(shù)正態(tài)分布法：適用于對(duì)數(shù)正態(tài)分布資料。

　　雙側(cè)界值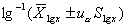：；單側(cè)上界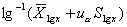：，或單側(cè)下界：。

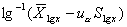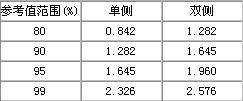
　　常用u值可根據(jù)要求由表3.2查出。

　　（3）百分位數(shù)法：常用于偏態(tài)分布資料以及資料中一端或兩端無(wú)確切數(shù)值的資料。

　　雙側(cè)界值：P2.5和P97.5；單側(cè)上界：P95，或單側(cè)下界：P5。

　　表：常用u值表

　　3．正態(tài)分布是許多統(tǒng)計(jì)方法的理論基礎(chǔ)：如t分布、F分布、分布都是在正態(tài)分布的基礎(chǔ)上推導(dǎo)出來的，u檢驗(yàn)也是以正態(tài)分布為基礎(chǔ)的。此外，t分布、二項(xiàng)分布、Poisson分布的極限為正態(tài)分布，在一定條件下，可以按正態(tài)分布原理來處理。

來自"

如果您認(rèn)為本條目還有待完善，需要補(bǔ)充新內(nèi)容或修改錯(cuò)誤內(nèi)容，請(qǐng)編輯條目。

-------------------------------------------------------------------------------------

http://baike.baidu.com/view/45379.html?wtp=tt

正態(tài)分布

　　normal distribution

　　一種概率分布。正態(tài)分布是具有兩個(gè)參數(shù)μ和σ2的連續(xù)型隨機(jī)變量的分布，第一參數(shù)μ是服從正態(tài)分布的隨機(jī)變量的均值，第二個(gè)參數(shù)σ2是此隨機(jī)變量的方差，所以正態(tài)分布記作N(μ，σ2 )。服從正態(tài)分布的隨機(jī)變量的概率規(guī)律為取與μ鄰近的值的概率大，而取離μ越遠(yuǎn)的值的概率越小；σ越小，分布越集中在μ附近，σ越大，分布越分散。正態(tài)分布的密度函數(shù)的特點(diǎn)是：關(guān)于μ對(duì)稱，在μ處達(dá)到最大值，在正（負(fù)）無(wú)窮遠(yuǎn)處取值為0，在μ±σ處有拐點(diǎn)。它的形狀是中間高兩邊低，圖像是一條位于x軸上方的鐘形曲線。當(dāng)μ＝0，σ2 ＝1時(shí)，稱為標(biāo)準(zhǔn)正態(tài)分布，記為N（0，1）。μ維隨機(jī)向量具有類似的概率規(guī)律時(shí)，稱此隨機(jī)向量遵從多維正態(tài)分布。多元正態(tài)分布有很好的性質(zhì)，例如，多元正態(tài)分布的邊緣分布仍為正態(tài)分布，它經(jīng)任何線性變換得到的隨機(jī)向量仍為多維正態(tài)分布，特別它的線性組合為一元正態(tài)分布。

　　正態(tài)分布最早由A.棣莫弗在求二項(xiàng)分布的漸近公式中得到。C.F.高斯在研究測(cè)量誤差時(shí)從另一個(gè)角度導(dǎo)出了它。P.S.拉普拉斯和高斯研究了它的性質(zhì)。

　　生產(chǎn)與科學(xué)實(shí)驗(yàn)中很多隨機(jī)變量的概率分布都可以近似地用正態(tài)分布來描述。例如，在生產(chǎn)條件不變的情況下，產(chǎn)品的強(qiáng)力、抗壓強(qiáng)度、口徑、長(zhǎng)度等指標(biāo)；同一種生物體的身長(zhǎng)、體重等指標(biāo)；同一種種子的重量；測(cè)量同一物體的誤差；彈著點(diǎn)沿某一方向的偏差；某個(gè)地區(qū)的年降水量；以及理想氣體分子的速度分量，等等。一般來說，如果一個(gè)量是由許多微小的獨(dú)立隨機(jī)因素影響的結(jié)果，那么就可以認(rèn)為這個(gè)量具有正態(tài)分布（見中心極限定理）。從理論上看，正態(tài)分布具有很多良好的性質(zhì) ，許多概率分布可以用它來近似；還有一些常用的概率分布是由它直接導(dǎo)出的，例如對(duì)數(shù)正態(tài)分布、t分布、F分布等。

　　正態(tài)分布應(yīng)用最廣泛的連續(xù)概率分布，其特征是“鐘”形曲線。

　　from http://www.5yiso.cn

　　(一)正態(tài)分布

　　1.正態(tài)分布

　　若的密度函數(shù)（頻率曲線）為正態(tài)函數(shù)（曲線）

　　(3-1)

　　則稱服從正態(tài)分布，記號(hào) ～。其中、是兩個(gè)不確定常數(shù)，是正態(tài)分布的參數(shù)，不同的、不同的對(duì)應(yīng)不同的正態(tài)分布。

　　正態(tài)曲線呈鐘型，兩頭低，中間高，左右對(duì)稱，曲線與橫軸間的面積總等于1。

　　2．正態(tài)分布的特征

　　服從正態(tài)分布的變量的頻數(shù)分布由、完全決定。

　　(1) 是正態(tài)分布的位置參數(shù)，描述正態(tài)分布的集中趨勢(shì)位置。正態(tài)分布以為對(duì)稱軸，左右完全對(duì)稱。正態(tài)分布的均數(shù)、中位數(shù)、眾數(shù)相同，均等于。

　　(2) 描述正態(tài)分布資料數(shù)據(jù)分布的離散程度，越大，數(shù)據(jù)分布越分散，越小，數(shù)據(jù)分布越集中。也稱為是正態(tài)分布的形狀參數(shù)，越大，曲線越扁平，反之，越小，曲線越瘦高。

　　(二)標(biāo)準(zhǔn)正態(tài)分布

　　1．標(biāo)準(zhǔn)正態(tài)分布是一種特殊的正態(tài)分布，標(biāo)準(zhǔn)正態(tài)分布的μ和σ2為0和1，通常用（或Z）表示服從標(biāo)準(zhǔn)正態(tài)分布的變量，記為 Z～N（0，1）。

　　2．標(biāo)準(zhǔn)化變換：此變換有特性：若原分布服從正態(tài)分布，則Z=(x-μ)/σ ～ N(0,1) 就服從標(biāo)準(zhǔn)正態(tài)分布,通過查標(biāo)準(zhǔn)正態(tài)分布表就可以直接計(jì)算出原正態(tài)分布的概率值。故該變換被稱為標(biāo)準(zhǔn)化變換。

　　3. 標(biāo)準(zhǔn)正態(tài)分布表

　　標(biāo)準(zhǔn)正態(tài)分布表中列出了標(biāo)準(zhǔn)正態(tài)曲線下從-∞到X(當(dāng)前值）范圍內(nèi)的面積比例。

　　（三）正態(tài)曲線下面積分布

　　1．實(shí)際工作中，正態(tài)曲線下橫軸上一定區(qū)間的面積反映該區(qū)間的例數(shù)占總例數(shù)的百分比，或變量值落在該區(qū)間的概率（概率分布）。不同范圍內(nèi)正態(tài)曲線下的面積可用公式3-2計(jì)算。

　　（3-2）

　　。

　　2.幾個(gè)重要的面積比例

　　軸與正態(tài)曲線之間的面積恒等于1。正態(tài)曲線下，橫軸區(qū)間（μ-σ，μ+σ）內(nèi)的面積為68.27%，橫軸區(qū)間（μ-1.96σ，μ+1.96σ）內(nèi)的面積為95.00%，橫軸區(qū)間（μ-2.58σ，μ+2.58σ）內(nèi)的面積為99.00%。

　　（四）正態(tài)分布的應(yīng)用

　　某些醫(yī)學(xué)現(xiàn)象，如同質(zhì)群體的身高、紅細(xì)胞數(shù)、血紅蛋白量，以及實(shí)驗(yàn)中的隨機(jī)誤差，呈現(xiàn)為正態(tài)或近似正態(tài)分布；有些指標(biāo)（變量）雖服從偏態(tài)分布，但經(jīng)數(shù)據(jù)轉(zhuǎn)換后的新變量可服從正態(tài)或近似正態(tài)分布，可按正態(tài)分布規(guī)律處理。其中經(jīng)對(duì)數(shù)轉(zhuǎn)換后服從正態(tài)分布的指標(biāo)，被稱為服從對(duì)數(shù)正態(tài)分布。

　　1. 估計(jì)頻數(shù)分布一個(gè)服從正態(tài)分布的變量只要知道其均數(shù)與標(biāo)準(zhǔn)差就可根據(jù)公式（3-2）估計(jì)任意取值范圍內(nèi)頻數(shù)比例。

　　2. 制定參考值范圍

　　（1）正態(tài)分布法適用于服從正態(tài)（或近似正態(tài)）分布指標(biāo)以及可以通過轉(zhuǎn)換后服從正態(tài)分布的指標(biāo)。

　　（2）百分位數(shù)法常用于偏態(tài)分布的指標(biāo)。表3-1中兩種方法的單雙側(cè)界值都應(yīng)熟練掌握。

　　表3-1 常用參考值范圍的制定

　　概率

　　（%）正態(tài)分布法百分位數(shù)法

　　雙側(cè) 單側(cè) 雙側(cè) 單側(cè)

　　下限上限下限上限

　　3. 質(zhì)量控制：為了控制實(shí)驗(yàn)中的測(cè)量（或?qū)嶒?yàn)）誤差，常以作為上、下警戒值，以作為上、下控制值。這樣做的依據(jù)是：正常情況下測(cè)量（或?qū)嶒?yàn)）誤差服從正態(tài)分布。

　　4. 正態(tài)分布是許多統(tǒng)計(jì)方法的理論基礎(chǔ)。檢驗(yàn)、方差分析、相關(guān)和回歸分析等多種統(tǒng)計(jì)方法均要求分析的指標(biāo)服從正態(tài)分布。許多統(tǒng)計(jì)方法雖然不要求分析指標(biāo)服從正態(tài)分布，但相應(yīng)的統(tǒng)計(jì)量在大樣本時(shí)近似正態(tài)分布，因而大樣本時(shí)這些統(tǒng)計(jì)推斷方法也是以正態(tài)分布為理論基礎(chǔ)的。

　　from http://www.foodmate.net/lesson/41/3-1.php

　　一、正態(tài)分布的概念

　　由表1.1的頻數(shù)表資料所繪制的直方圖，圖3.1（1）可以看出，高峰位于中部，左右兩側(cè)大致對(duì)稱。我們?cè)O(shè)想，如果觀察例數(shù)逐漸增多，組段不斷分細(xì)，直方圖頂端的連線就會(huì)逐漸形成一條高峰位于中央（均數(shù)所在處），兩側(cè)逐漸降低且左右對(duì)稱，不與橫軸相交的光滑曲線圖3.1（3）。這條曲線稱為頻數(shù)曲線或頻率曲線，近似于數(shù)學(xué)上的正態(tài)分布（normal distribution）。由于頻率的總和為100%或1，故該曲線下橫軸上的面積為100%或1。

　　圖3.1頻數(shù)分布逐漸接近正態(tài)分布示意圖

　　為了應(yīng)用方便，常對(duì)正態(tài)分布變量X作變量變換。

　　（3.1）

　　該變換使原來的正態(tài)分布轉(zhuǎn)化為標(biāo)準(zhǔn)正態(tài)分布 (standard normal distribution)，亦稱u分布。u被稱為標(biāo)準(zhǔn)正態(tài)變量或標(biāo)準(zhǔn)正態(tài)離差（standard normal deviate）。

　　二、正態(tài)分布的特征：

　　1．正態(tài)曲線（normal curve）在橫軸上方均數(shù)處最高。

　　2．正態(tài)分布以均數(shù)為中心，左右對(duì)稱。

　　3．正態(tài)分布有兩個(gè)參數(shù)，即均數(shù)和標(biāo)準(zhǔn)差。是位置參數(shù)，當(dāng)固定不變時(shí)，越大，曲線沿橫軸越向右移動(dòng)；反之，越小，則曲線沿橫軸越向左移動(dòng)。是形狀參數(shù)，當(dāng)固定不變時(shí)，越大，曲線越平闊；越小，曲線越尖峭。通常用表示均數(shù)為，方差為的正態(tài)分布。用N（0，1）表示標(biāo)準(zhǔn)正態(tài)分布。

　　4．正態(tài)曲線下面積的分布有一定規(guī)律。

　　實(shí)際工作中，常需要了解正態(tài)曲線下橫軸上某一區(qū)間的面積占總面積的百分?jǐn)?shù)，以便估計(jì)該區(qū)間的例數(shù)占總例數(shù)的百分?jǐn)?shù)（頻數(shù)分布）或觀察值落在該區(qū)間的概率。正態(tài)曲線下一定區(qū)間的面積可以通過附表1求得。對(duì)于正態(tài)或近似正態(tài)分布的資料，已知均數(shù)和標(biāo)準(zhǔn)差，就可對(duì)其頻數(shù)分布作出概約估計(jì)。

　　查附表1應(yīng)注意：①表中曲線下面積為-∞到u的左側(cè)累計(jì)面積；②當(dāng)已知μ、σ和X時(shí)先按式（3.1）求得u值，再查表，當(dāng)μ、σ未知且樣本含量n足夠大時(shí)，可用樣本均數(shù)和標(biāo)準(zhǔn)差S分別代替μ和σ，按式求得u值，再查表；③曲線下對(duì)稱于0的區(qū)間面積相等，如區(qū)間（-∞，-1.96）與區(qū)間（1.96，∞）的面積相等，④曲線下橫軸上的總面積為100%或1。

　　正態(tài)分布曲線下有三個(gè)區(qū)間的面積應(yīng)用較多，應(yīng)熟記：①標(biāo)準(zhǔn)正態(tài)分布時(shí)區(qū)間（-1,1）或正態(tài)分布時(shí)區(qū)間（μ-1σ,μ+1σ）的面積占總面積的68.27%；②標(biāo)準(zhǔn)正態(tài)分布時(shí)區(qū)間（-1.96,1.96）或正態(tài)分布區(qū)間（μ-1.96σ,μ+1.96σ）的面積占總面積的95%；③標(biāo)準(zhǔn)正態(tài)分布時(shí)區(qū)間（-2.58,2.58）或正態(tài)分布時(shí)區(qū)間（μ-2.58σ,μ+2.58σ）的面積占總面積的99%。如圖3.2所示。（μ-3σ）的面積比例為99.74%,(μ-2σ)面積比例為95.44%。

　　圖3.2 正態(tài)曲線與標(biāo)準(zhǔn)正態(tài)曲線的面積分布

posted @ 2009-03-12 23:08 donnie 閱讀(961) | 評(píng)論 (0) | 編輯收藏

均值

http://baike.baidu.com/view/1052684.htm

均值

　　統(tǒng)計(jì)學(xué)術(shù)語(yǔ)，與“平均”（***erage）意義相同。例如： l、3、6，10、20這5個(gè)數(shù)字的均值是8。

posted @ 2009-03-12 22:55 donnie 閱讀(147) | 評(píng)論 (0) | 編輯收藏

方差(Variance)

http://wiki.mbalib.com/wiki/%E6%96%B9%E5%B7%AE

方差(Variance)

什么是方差

　　方差和標(biāo)準(zhǔn)差是測(cè)度數(shù)據(jù)變異程度的最重要、最常用的指標(biāo)。

　　方差是各個(gè)數(shù)據(jù)與其算術(shù)平均數(shù)的離差平方和的平均數(shù)，通常以 $σ 2$ 表示。方差的計(jì)量單位和量綱不便于從經(jīng)濟(jì)意義上進(jìn)行解釋，所以實(shí)際統(tǒng)計(jì)工作中多用方差的算術(shù)平方根——標(biāo)準(zhǔn)差來測(cè)度統(tǒng)計(jì)數(shù)據(jù)的差異程度。

　　標(biāo)準(zhǔn)差又稱均方差，一般用σ表示。方差和標(biāo)準(zhǔn)差的計(jì)算也分為簡(jiǎn)單平均法和加權(quán)平均法，另外，對(duì)于總體數(shù)據(jù)和樣本數(shù)據(jù)，公式略有不同。

方差的計(jì)算公式

　　設(shè)總體方差為 $σ 2$ ，對(duì)于未經(jīng)分組整理的原始數(shù)據(jù)，方差的計(jì)算公式為：

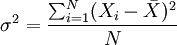
　　 $\sigma^2=\frac{\sum_{i=1}^N(X_i-\bar{X})^2}{N}$

　　對(duì)于分組數(shù)據(jù)，方差的計(jì)算公式為：

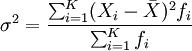
　　 $\sigma^2=\frac{\sum_{i=1}^K(X_i-\bar{X})^2 f_i}{\sum_{i=1}^K f_i}$

　　方差的平方根即為標(biāo)準(zhǔn)差，其相應(yīng)的計(jì)算公式為：

　　未分組數(shù)據(jù)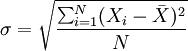： $\sigma=\sqrt{\frac{\sum_{i=1}^N(X_i-\bar{X})^2}{N}}$

　　分組數(shù)據(jù)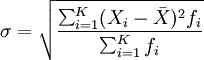： $\sigma=\sqrt{\frac{\sum_{i=1}^K(X_i-\bar{X})^2 f_i}{\sum_{i=1}^K f_i}}$

[編輯]

樣本方差和標(biāo)準(zhǔn)差

　　樣本方差與總體方差在計(jì)算上的區(qū)別是：總體方差是用數(shù)據(jù)個(gè)數(shù)或總頻數(shù)去除離差平方和，而樣本方差則是用樣本數(shù)據(jù)個(gè)數(shù)或總頻數(shù)減1去除離差平方和，其中樣本數(shù)據(jù)個(gè)數(shù)減1即n－1稱為自由度。設(shè)樣本方差為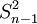 $S_{n-1}^2$ ，根據(jù)未分組數(shù)據(jù)和分組數(shù)據(jù)計(jì)算樣本方差的公式分別為：

　　未分組數(shù)據(jù)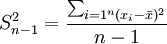： $S_{n-1}^2=\frac{\sum_{i=1^n(x_i-\bar{x})^2}}{n-1}$

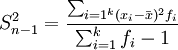
　　分組數(shù)據(jù)： $S_{n-1}^2=\frac{\sum_{i=1^k(x_i-\bar{x})^2 f_i}}{\sum_{i=1}^k f_i-1}$

　　未分組數(shù)據(jù)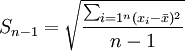： $S_{n-1}=\sqrt{\frac{\sum_{i=1^n(x_i-\bar{x})^2}}{n-1}}$

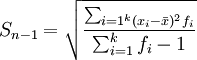
　　分組數(shù)據(jù)： $S_{n-1}=\sqrt{\frac{\sum_{i=1^k(x_i-\bar{x})^2 f_i}}{\sum_{i=1}^k f_i-1}}$

　　例:考察一臺(tái)機(jī)器的生產(chǎn)能力，利用抽樣程序來檢驗(yàn)生產(chǎn)出來的產(chǎn)品質(zhì)量，假設(shè)搜集的數(shù)據(jù)如下：

3.43	3.45	3.43	3.48	3.52	3.50	3.39
3.48	3.41	3.38	3.49	3.45	3.51	3.50

　　根據(jù)該行業(yè)通用法則：如果一個(gè)樣本中的14個(gè)數(shù)據(jù)項(xiàng)的方差大于0.005，則該機(jī)器必須關(guān)閉待修。問此時(shí)的機(jī)器是否必須關(guān)閉？

　　解：根據(jù)已知數(shù)據(jù)，計(jì)算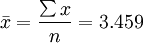 $\bar{x}=\frac{\sum x}{n}=3.459$

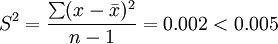
　　 $S^2=\frac{\sum(x-\bar{x})^2}{n-1}=0.002<0.005$

　　因此，該機(jī)器工作正常。

　　方差和標(biāo)準(zhǔn)差也是根據(jù)全部數(shù)據(jù)計(jì)算的，它反映了每個(gè)數(shù)據(jù)與其均值相比平均相差的數(shù)值，因此它能準(zhǔn)確地反映出數(shù)據(jù)的離散程度。方差和標(biāo)準(zhǔn)差是實(shí)際中應(yīng)用最廣泛的離散程度測(cè)度值。

---------------------------------------------------------------------
http://zh.wikipedia.org/wiki/%E6%96%B9%E5%B7%AE

方差

維基百科，自由的百科全書

跳轉(zhuǎn)到: 導(dǎo)航, 搜索

在概率論和統(tǒng)計(jì)學(xué)中，一個(gè)隨機(jī)變量的“方差”描述的是它的離散程度，也就是該變量離其期望值的距離。一個(gè)實(shí)隨機(jī)變量的方差也稱為它的二階距，恰巧也是它的二階culmulent。方差的算術(shù)平方根稱為該隨機(jī)變量的標(biāo)準(zhǔn)差。

[編輯] 定義

設(shè) $X$ 為服從分布 $F$ 的隨機(jī)變量，則稱 $V a r (X) = E (X - E X) 2$ 為隨機(jī)變量 $X$ 或者分布 $F$ 的方差。

如果 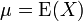$\mu = \operatorname{E}(X)$ 是隨機(jī)變數(shù) X 的期望值 (平均數(shù)) , 則其變異數(shù)為: $\operatorname{var}(X) = \operatorname{E}( ( X - \mu ) ^ 2 ).$

[編輯] 特性

在樣本空間Ω上存在有限期望和方差的隨機(jī)變量構(gòu)成一個(gè)希爾伯特空間： L^2(Ω, dP)，不過這里的內(nèi)積和長(zhǎng)度跟方差，標(biāo)準(zhǔn)差還是不大一樣。所以，我們得把這個(gè)空間“除”常變量構(gòu)成的子空間，也就是說把相差一個(gè)常數(shù)的所有原來那個(gè)空間的隨機(jī)變量做成一個(gè)等價(jià)類。這還是一個(gè)新的無(wú)窮維線性空間，并且有一個(gè)從老空間內(nèi)積誘導(dǎo)出來的新內(nèi)積，而這個(gè)內(nèi)積就是方差

[編輯] 一般化

如果X是一個(gè)向量其取值范圍在Rⁿ空間，并且其每個(gè)元素都是一個(gè)一維隨機(jī)變量，我們就把X稱為隨機(jī)向量。隨機(jī)向量的方差是一維隨機(jī)變量方差的自然推廣，其定義為E[(X − μ)(X − μ)^T], 其中 μ = E(X) ，X^T是X的轉(zhuǎn)秩. 這個(gè)方差是一個(gè)非負(fù)定方陣，通常稱為協(xié)方差矩陣。

如果X是一個(gè)復(fù)隨機(jī)變量，那么其方差定義則為E[(X − μ)(X − μ)^*], 其中X^*是X的復(fù)共軛向量。根據(jù)這個(gè)定義，方差為實(shí)數(shù)。

[編輯] 歷史

方差這個(gè)詞首先由Ronald Fisher在論文The Correlation Between Relatives on the Supposition of Mendelian Inheritance中引入.

[編輯] 參考出處

^ Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. (1986) Numerical recipes: The art of scientific computing. Cambridge: Cambridge University Press. (online)

posted @ 2009-03-12 22:51 donnie 閱讀(10899) | 評(píng)論 (0) | 編輯收藏

有計(jì)劃的學(xué)習(xí)。

工作若干年以來，荒廢了太多時(shí)間，昨天上課聽項(xiàng)目管理老師講到計(jì)劃，何不把日常學(xué)習(xí)也來計(jì)劃一下呢。
于是，訂計(jì)劃若干，時(shí)間涵蓋工作時(shí)間、晚上。唯無(wú)人監(jiān)督，看我能堅(jiān)持多久，做記號(hào)。

posted @ 2009-03-09 22:09 donnie 閱讀(78) | 評(píng)論 (0) | 編輯收藏

日語(yǔ)初次接觸

看cd學(xué)日語(yǔ)，大概瀏覽了一下，寫法并不是十分特殊，要記的基礎(chǔ)比較多，發(fā)音要適應(yīng)一下。

posted @ 2009-03-09 22:05 donnie 閱讀(81) | 評(píng)論 (0) | 編輯收藏

redhat linux 9 軟raid恢復(fù)

起因：掉電。
現(xiàn)象：系統(tǒng)文件多找不到。
恢復(fù)：嘗試修復(fù)文件系統(tǒng)，失敗；
            安裝盤引導(dǎo)修復(fù)，失敗；
            安裝盤引導(dǎo)，覆蓋安裝，失敗；
           安裝盤引導(dǎo)，全新安裝，成功。tips: 定制安裝；手動(dòng)設(shè)置分區(qū)，保留原raid設(shè)置。

posted @ 2009-02-25 18:30 donnie 閱讀(109) | 評(píng)論 (0) | 編輯收藏

僅列出標(biāo)題

常用鏈接

留言簿

隨筆分類(66)

隨筆檔案(79)

相冊(cè)

收藏夾(11)

搜索

積分與排名

最新隨筆

最新評(píng)論

閱讀排行榜

正態(tài)分布

出自MBA智庫(kù)百科(http://wiki.mbalib.com/)

目錄

什么是正態(tài)分布

正態(tài)分布的發(fā)展

正態(tài)分布的主要特征

正態(tài)分布的應(yīng)用

正態(tài)分布

http://baike.baidu.com/view/1052684.htm

均值

什么是方差

方差的計(jì)算公式

樣本方差和標(biāo)準(zhǔn)差

方差

維基百科，自由的百科全書

目錄

[編輯] 定義

[編輯] 特性

[編輯] 一般化

[編輯] 歷史

[編輯] 參考出處