亚洲网址在线观看,亚洲国产精品毛片av不卡在线,国产l精品国产亚洲区在线观看

URAL 1011

ZelluX — Wed, 23 Apr 2008 14:44:00 GMT

Problem

Every bus in the Ekaterinburg city has a special man (or woman) called conductor. When you ride the bus, you have to give money to the conductor. We know that there are more then P% conductors and less then Q% conductors. Your task is to determine a minimal possible number of Ekaterinburg citizens.

我只能说太挫了。。。精度问题搞了半天，看来��点�q�是要尽量化成整型再��啊�?br />

�q�有个问题就是q*i是开区间�q�是闭区��_��M��Wrong Answer了无数次后�ȝ��q�了。。�?br />

ZelluX 2008-04-23 22:44 发表评论

URAL 题解 - wiki

ZelluX — Thu, 17 Apr 2008 03:48:00 GMT

http://www.nocow.cn/index.php

抽时间多做做�Q�提高下我可怜的��法功底 >,<

ZelluX 2008-04-17 11:48 发表评论

《编�E�之��》上的一道题目的讨论

ZelluX — Mon, 14 Apr 2008 16:23:00 GMT

计算机科学论坛最�q��D办了一个阅��L��章，提交书评的活动，具体内容误��http://www.ieee.org.cn/dispbbs.asp?boardID=42&ID=61162�?/p>

�q�里我想针对��L��上的一个问题谈谈自��q��理解�?/p>

问题很简单，求二�q�制�?的个数。对于一个字节（8bit�Q�的变量�Q�求其二�q�制表示�?1"的个敎ͼ�要求��法的执行效率尽可能的高�?/p>

先来看看��L��上给出的几个��法�Q?/p>

解法一�Q�每�ơ除二，看是否�ؓ奇数�Q�是的话��q��计加一�Q�最后这个结果就是二�q�制表示�?的个数�?/p>

解法二，同样用到一个��@环，只是里面的操作用位移操作��化了�?/p>

   1: int Count(int v)
   2: {
   3:      int num = 0;
   4:      while (v) {
   5:          num += v & 0x01;
   6:          v >>= 1;
   7:      }
   8:      return num;
   9: }

解法三，用到一个��y妙的与操作，v & (v -1 )每次能消��M��q�制表示中最后一�?�Q�利用这个技巧可以减��一定的循环�ơ数�?/p>

解法四，查表法，因�ؓ只有数据8bit�Q�直接徏一张表�Q�包含各个数�?的个敎ͼ�然后查表��p��。复杂度O(1)�?/p>

   1: int countTable[256] = { 0, 1, 1, 2, 1, ..., 7, 7, 8 };
   2:
   3: int Count(int v) {
   4:      return countTable[v];
   5: }

好了�Q�这��是��L��上给出的四种�Ҏ��Q�下面谈谈我的看法�?/p>

首先是对��法的衡量上�Q�复杂度真的是唯一的标准吗�Q�尤其对于这�U�数据规模给定，而且很小的情况下�Q�复杂度其实是个比较�ơ要的因素�?/p>

查表法的复杂度�ؓO(1)�Q�我用解法一�Q��@环八�ơ固定，复杂度也是O(1)。至于数据规模变大，变成32位整型，那查表法自然也不合适了�?/p>

其次�Q�我觉得既然是这样一个很��的操作�Q�衡量的��度也必然要��，CPU旉��周期可以作�ؓ一个参考�?/p>

解法一里有若干�ơ整数加法，若干�ơ整数除法（一般的�~�译器都能把它优化成位移�Q�，�q�有几个循环分支判断�Q�几个奇偶性判断（�q�个比较耗时��_��Ҏ��CSAPP上的数据�Q�一般一个branch penalty得耗掉14个左右的cycle�Q�，加�v来大概几十个cycle吧�?/p>

再看解法四，查表法看��g��ơ地址计算��p��解决�Q�但实际上这里用��C��个访存操作，而且�W�一�ơ访存的时候很有可能那个数�l�不在cache里，�q�样一个cache miss��D��的后果可能就是耗去几十甚至上百个cycle�Q�因��讉K��内存�Q�。所以对于这�U�“小操作”，�q�个��法的性能其实是很差的�?/p>

�q�里我再推荐几个解决�q�个问题的算法，�?2位无�W�号整型��Z��?/p>

   1: int Count(unsigned x) {
   2:     x = x - ((x >> 1) & 0x55555555);
   3:     x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
   4:     x = (x + (x >> 4)) & 0x0F0F0F0F;
   5:     x = x + (x >> 8);
   6:     x = x + (x >> 16);
   7:     return x & 0x0000003F;
   8: }

�q�里用的是二分法�Q�两两一�l�相加，之后四个四个一�l�相加，接着八个八个�Q�最后就得到各位之和了�?/p>

�q�有一个更巧妙的HAKMEM��法

   1: int Count(unsigned x) {
   2:     unsigned n;
   3:
   4:     n = (x >> 1) & 033333333333;
   5:     x = x - n;
   6:     n = (n >> 1) & 033333333333;
   7:     x = x - n;
   8:     x = (x + (x >> 3)) & 030707070707;
   9:     x = modu(x, 63);
   10:     return x;
   11: }

首先是将二进制各位三个一�l�，求出每组�?的个敎ͼ�然后盔R��两组归�ƈ�Q�得到六个一�l�的1的个敎ͼ�最后很巧妙的用�?3取余得到了结果�?/p>

因�ؓ2^6 = 64�Q�也��是�?x_0 + x_1 * 64 + x_2 * 64 * 64 = x_0 + x_1 + x_2 (mod 63)�Q�这里的�{�号表示同余�?/p>

�q�个�E�序只需要十条左��x��令，而且不访存，速度很快�?/p>

由此可见�Q�衡量一个算法实际效果不单要看复杂度�Q�还要结合其他情况具体分析�?/p>

关于后面的两道扩展问题，问题一是问32位整型如何处理，�q�个上面已经讲了�?/p>

问题二是�l�定两个整数A和B�Q�问A和B有多��位是不同的�?/p>

�q�个问题其实��是�?问题多了一个步骤，只要先算出A和B的异或结果，然后求这个��g��1的个数就行了�?br />
��M��看来�q�本书还是很不错的，比较喜欢里面针对一个问题提��Z��同算法�ƈ不断改进的风根{��这里提��Z��点个人的理解�Q�望大家指正 ;-)

(by ZelluX http://m.tkk7.com/zellux)

ZelluX 2008-04-15 00:23 发表评论

ZelluX — Wed, 09 Apr 2008 16:33:00 GMT

摘要: 问题�Q?
�l�定n�?2位无�W�号整数�Q�求出其中异或结果最大的两个整数�?nbsp; 阅读全文

ZelluX 2008-04-10 00:33 发表评论

SICP 习题记录 (1)

ZelluX — Thu, 03 Apr 2008 14:33:00 GMT

没事�q�找了几个SICP上的习题做，先是一道以前只惛_��一�U�很啰嗦的写法的题目

Ex 2.18
把一个列表倒过来。不习惯在lisp里用iterative方式 >,<

接下来几题都是Map-Reduce思想的应用（或者照书上的说法，用enumerator - filter - map - accumulator�q�四个步骤操作一个list�Q?br />
用到的几个函敎ͼ�

enumrate-tree 的功能是遍历一个树状结构，把其中的所有叶子保存在一个list中�?br />
Ex 2.34
利用Horner's rule计算多项式结果（�q�公式这几天�q�经常碰刎ͼ�

Ex 2.35
数出一��|��中的叶子数。这题我的做法比较土�Q�没惛_��map-reduce操作上的递归�Q�而是把叶子节点的值都�Ҏ��1然后一个篏加�?/p>

其实只要递归调用��d��数就行了

Ex 2.36
可以理解��矩阵各列之和吧

> (accumulate-n + 0 (list (list 1 2 3) (list 4 5 6) (list 7 8 9) (list 10 11 12)))
(22 26 30)

ZelluX 2008-04-03 22:33 发表评论

ZelluX — Wed, 26 Mar 2008 16:21:00 GMT

其实理解了 Regular Expression -> NFA -> DFA �q�个�q�程�Q�大致的复杂度确定也不难

发信�? styc (styc), 信区: Algorithm
标�?�? Re: 请问一下大家正则表辑ּ�的时间复杂度
发信�? 水木�C�֌� (Wed Mar 26 20:37:02 2008), 站内

NFA构造O(n)�Q�匹配O(nm)
DFA构造O(2^n)�Q�最��化O(kn'logn')�Q�N'=O(2^n)�Q�，匚w��O(m)
n=regex长度�Q�m=串长�Q�k=字母表大��，n'=原始的dfa大小
大概是这样子�?br />

ZelluX 2008-03-27 00:21 发表评论

Minesweeper is NP-complete

ZelluX — Wed, 06 Feb 2008 11:40:00 GMT

http://web.mat.bham.ac.uk/R.W.Kaye/minesw/ordmsw.htm

居然是NPC...

ZelluX 2008-02-06 19:40 发表评论

Tom Duff on Duff's Device

ZelluX — Thu, 29 Nov 2007 08:02:00 GMT

Subject: Re: Explanation, please!
Summary: Original citation
From: td@alice.UUCP (Tom Duff)
Organization: AT&T Bell Laboratories, Murray Hill NJ
Date: 29 Aug 88 20:33:51 GMT
Message-ID: <8144@alice.UUCP>

I normally do not read comp.lang.c, but Jim McKie told me that ``'' had come up in comp.lang.c again. I have lost the version that was sent to netnews in May 1984, but I have reproduced below the note in which I originally proposed the device. (If anybody has a copy of the netnews version, I would gratefully receive a copy at research!td or td@research.att.com.)

To clear up a few points:

The point of the device is to express general loop unrolling directly in C. People who have posted saying `just use memcpy' have missed the point, as have those who have criticized it using various machine-dependent memcpy implementations as support. In fact, the example in the message is not implementable as memcpy, nor is any computer likely to have an memcpy-like idiom that implements it.

Somebody claimed that while the device was named for me, I probably didn't invent it. I almost certainly did invent it. I had definitely not seen or heard of it when I came upon it, and nobody has ever even claimed prior knowledge, let alone provided dates and times. Note the headers on the message below: apparently I invented the device on November 9, 1983, and was proud (or disgusted) enough to send mail to dmr. Please note that I do not claim to have invented loop unrolling, merely this particular expression of it in C.
The device is legal dpANS C. I cannot quote chapter and verse, but Larry Rosler, who was chairman of the language subcommittee (I think), has assured me that X3J11 considered it carefully and decided that it was legal. Somewhere I have a note from dmr certifying that all the compilers that he believes in accept it. Of course, the device is also legal C++, since Bjarne uses it in his book.
Somebody invoked (or more properly, banished) the `false god of efficiency.' Careful reading of my original note will put this slur to rest. The alternative to genuflecting before the god of code-bumming is finding a better algorithm. It should be clear that none such was available. If your code is too slow, you must make it faster. If no better algorithm is available, you must trim cycles.
The same person claimed that the device wouldn't exhibit the desired speed-up. The argument was flawed in two regards: first, it didn't address the performance of the device, but rather the performance of one of its few uses (implementing memcpy) for which many machines have a high-performance idiom. Second, the poster made his claims in the absence of timing data, which renders his assertion suspect. A second poster tried the test, but botched the implementation, proving only that with diligence it is possible to make anything run slowly.
Even Henry Spencer, who hit every other nail square on the end with the flat round thing stuck to it, made a mistake (albeit a trivial one). Here is Henry replying to bill@proxftl.UUCP (T. William Wells):
```
   >>... Dollars to doughnuts this
    >>was written on a RISC machine.
    >Nope.  Bell Labs Research uses VAXen and 68Ks, mostly.
    
```
I was at Lucasfilm when I invented the device.
Transformations like this can only be justified by measuring the resulting code. Be careful when you use this thing that you don't unwind the loop so much that you overflow your machine's instruction cache. Don't try to be smarter than an over-clever C compiler that recognizes loops that implement block move or block clear and compiles them into machine idioms.

Here then, is the original document describing Duff's device:

From research!ucbvax!dagobah!td Sun Nov 13 07:35:46 1983
Received: by ucbvax.ARPA (4.16/4.13) id AA18997; Sun, 13 Nov 83 07:35:46 pst
Received: by dagobah.LFL (4.6/4.6b) id AA01034; Thu, 10 Nov 83 17:57:56 PST
Date: Thu, 10 Nov 83 17:57:56 PST
From: ucbvax!dagobah!td (Tom Duff)
Message-Id: <8311110157.AA01034@dagobah.LFL>
To: ucbvax!decvax!hcr!rrg, ucbvax!ihnp4!hcr!rrg, ucbvax!research!dmr, ucbvax!research!rob

Consider the following routine, abstracted from code which copies an array of shorts into the Programmed IO data register of an Evans & Sutherland Picture System II:

 
send(to, from, count)

register short *to, *from;

register count;

{

    do

        *to = *from++;

    while (--count>0);

}

(Obviously, this fails if the count is zero.)
The VAX C compiler compiles the loop into 2 instructions (a movw and a sobleq,
I think.) As it turns out, this loop was the bottleneck in a real-time animation playback program which ran too slowly by about 50%. The standard way to get more speed out of something like this is to unwind the loop a few times, decreasing the number of sobleqs. When you do that, you wind up with a leftover partial loop. I usually handle this in C with a switch that indexes a list of copies of the original loop body. Of course, if I were writing assembly language code, I'd just jump into the middle of the unwound loop to deal with the leftovers. Thinking about this yesterday, the following implementation occurred to me:

send(to, from, count)
    register short *to, *from;
    register count;
{
    register n=(count+7)/8;
    switch(count%8) {
        case 0:    do {    *to = *from++;
        case 7:        *to = *from++;
        case 6:        *to = *from++;
        case 5:        *to = *from++;
        case 4:        *to = *from++;
        case 3:        *to = *from++;
        case 2:        *to = *from++;
        case 1:        *to = *from++;
        } while(--n>0);
    }
}

Disgusting, no? But it compiles and runs just fine. I feel a combination of pride and revulsion at this discovery. If no one's thought of it before, I think I'll name it after myself.

It amazes me that after 10 years of writing C there are still little corners that I haven't explored fully. (Actually, I have another revolting way to use switches to implement interrupt driven state machines but it's too horrid to go into.)

Many people (even bwk?) have said that the worst feature of C is that switches don't break automatically before each case label. This code forms some sort of argument in that debate, but I'm not sure whether it's for or against.

yrs trly
Tom

ZelluX 2007-11-29 16:02 发表评论

In-place Matrix Transposition

ZelluX — Mon, 12 Nov 2007 08:16:00 GMT

O(1)�I�间求矩阵�{�|�的��法�Q�貌似是分解成几个��@环群�Q�分别处理�?br /> from wikipedia

http://m.tkk7.com/Files/zellux/In-place_matrix_transposition.zip

ZelluX 2007-11-12 16:16 发表评论

后缀树的在线生成��法

ZelluX — Wed, 07 Nov 2007 13:08:00 GMT

�W�一�ơ接触后�~�树应该是在某�ơ省队集训，徐串大牛做的讲��?br /> 不过当时只是有了个印象�?br /> 现在发现�q�东东还是很好用�?nbsp; @,@

http://m.tkk7.com/Files/zellux/SuffixT1withFigs.rar

On–line construction of suffix trees
by Esko Ukkonen

Key Words.
Linear time algorithm, suffix tree, suffix trie, suffix automaton, DAWG.

Abstract.
An on–line algorithm is presented for constructing the suffix tree for a given string in time linear in the length of the string. The new algorithm has the desirable property of processing the string symbol by symbol from left to right. It has always the suffix tree for the scanned part of the string ready. The method is developed as a linear–time version of a very simple algorithm for (quadratic size) suffix tries. Regardless of its quadratic worst-case this latter algorithm can be a good practical method when the string is not too long. Another variation of this method is shown to give in a natural way the well–known algorithms for constructing suffix automata (DAWGs).

ZelluX 2007-11-07 21:08 发表评论

ZelluX — Wed, 07 Nov 2007 03:02:00 GMT

发现居然�q�是Pascal描述�Q�亲切啊亲切

http://iprai.hust.edu.cn/icl2002/algorithm/datastructure/basic/binary_tree/chapter5_4.htm

�U�烦二叉�?/h2>
�?a >用二叉链表作��Z��叉树的存储结�?/a>�Ӟ��因�ؓ每个�l�点中只有指向其左、右儿子�l�点的指针，所以从��M��l�点出发只能直接扑ֈ�该结点的左、右儿子。在一般情况下靠它无法直接扑ֈ�该结点在某种遍历序下的前驱和后��l�点。如果在每个�l�点中增加指向其前驱和后�l�结点的指针�Q�将降低存储�I�间的效率�?/p>
我们可以证明�Q�在n个结点的二叉链表中含有n+1个空指针。因为含n个结点的二叉链表中含有个指针�Q�除了根�l�点�Q�每个结炚w��有一个从父结�Ҏ��向该�l�点的指针，因此一�׃��用了n-1个指针，所以在n个结点的二叉链表中含有n+1个空指针�?/p>
因此可以利用�q�些�I�指针，存放指向�l�点在某�U�遍历次序下的前驱和后��l�点的指针。这�U�附加的指针�U�Cؓ�U�烦�Q�加上了�U�烦的二叉链表称�?font face="楷体_GB2312">�U�烦链表�Q�相应的二叉树称�?font face="楷体_GB2312">�U�烦二叉�?/font>。�ؓ了区分一个结点的指针是指向其儿子的指针，�q�是指向其前驱或后��l�点的线索，可在每个�l�点中增加两个线索标志。这��P��U�烦二叉树结点类型定义�ؓ�Q?/p>

type

TPosition=^thrNodeType;

thrNodeType=record

              Label:LabelType;

              ltag,rtag:0..1;

              LeftChild,RightChild:TPosition;

             end;

其中ltag为左�U�烦标志�Q�rtag为右�U�烦标志。它们的含义�?

ltag=0�Q�LeftChild是指向结点左儿子的指针；
ltag=1�Q�LeftChild是指向结点前��q��左线索�?br />
rtag=0�Q�RightChild是指向结点右儿子的指针；
rtag=1�Q�RihgtChild是指向结点后�l�的右线索�?

例如�?3(a)是一��中序线索二叉树�Q�它的线索链表如�?3(b)所�C��?/p>

(a)

(b)

�?3 �U�烦二叉树及其线索链�?/p>

�?3(b)中，在二叉树的线索链表上增加了一个头�l�点�Q�其LeftChild指针指向二叉树的根结点，其RightChild指针指向中序遍历时的最后一个结炏V��另外，二叉树中依中序列表的�W�一个结点的LeftChild指针�Q�和最后一个结点的RightChild指针都指向头�l�点。这��像��Z��叉树建立了一个双向线索链表，既可从第一个结点�v�Q�顺着后��q�行遍历�Q�也可从最后一个结点�v��着前驱�q�行遍历�?/p>
如何在线索二叉树中找�l�点的前驱和后��l�点�Q�以�?3的中序线索二叉树��Z��。树中所有叶�l�点的右链是�U�烦�Q�因此叶�l�点的RightChild指向该结点的后��l�点�Q�如�?3中结�?b"的后�l��ؓ�l�点""。当一个内部结点右�U�烦标志�?�Ӟ��其RightChild指针指向其右儿子�Q�因此无法由RightChild得到其后�l�结炏V��然而，�׃��序遍历的定义可知�Q�该�l�点的后�l�应是遍历其叛_��树时讉K��的第一个结点，卛_��子树中最左下的结炏V��例如在扄��?"的后�l�时�Q�首先沿��x��针找到其叛_��树的根结�?-"�Q�然后沿其LeftChild指针往下直臛_��左线索标志�ؓ1的结点，即�ؓ其后�l�结�?在图中是�l�点"c")。类似地�Q�在中序�U�烦树中扄��点的前驱�l�点的规律是�Q�若该结点的左线索标志�ؓ1�Q�则LeftChild为线索，直接指向其前��q��点，否则遍历左子树时最后访问的那个�l�点�Q�即左子树中最右下的结点�ؓ其前��q��炏V��由此可知，若线索二叉树的高度�ؓh�Q�则在最坏情况下�Q�可�?em>O(h)旉��内找��C��个结点的前驱或后�l�结炏V��在对中序线索二叉树�q�行遍历�Ӟ��无须像非�U�烦树的遍历那样�Q�利用递归引入栈来保存待访问的子树信息�?/p>
对一��非�U�烦二叉树以某种�ơ序遍历使其变�ؓ一��늺�索二叉树的过�E�称�?font face="楷体_GB2312">二叉树的�U�烦�?/font>。由于线索化的实质是��二叉链表中的空指针改�ؓ指向�l�点前驱或后�l�的�U�烦�Q�而一个结点的前驱或后�l�结点的信息只有在遍历时才能得到�Q�因此线索化的过�E�即为在遍历�q�程中修改空指针的过�E�。�ؓ了记下遍历过�E�中讉K��l�点的先后次序，可附设一个指针pre始终指向刚刚讉K��q�的�l�点。当指针p指向当前讉K��的结�Ҏ��Q�pre指向它的前驱。由此也可推知pre所指结点的后��为p所指的当前�l�点。这样就可在遍历�q�程中将二叉树线索化。对于找前驱和后�l�结点这二种�q�算而言�Q�线索树优于非线索树。但�U�烦树也有其�~�点。在�q�行插�h和删除操作时�Q�线索树比非�U�烦树的旉��开销大。原因在于在�U�烦树中�q�行插�h和删除时�Q�除了修改相应的指针外，�q�要修改相应的线索�?/p>

ZelluX 2007-11-07 11:02 发表评论

ZelluX — Wed, 31 Oct 2007 10:11:00 GMT

摘要: 问题�Q?
有两堆石子，数量��L��Q�可以不同。游戏开始由两个��取矛_��。游戏规定，每次有两�U�不同的取法�Q�一是可以在��L��的一堆中取走��L��多的矛_��Q�二是可以在两堆中同时取走相同数量的矛_��。最后把矛_��全部取完者�ؓ胜者。现在给出初始的两堆矛_��的数目，如果轮到你先取，假设双方都采取最好的�{�略�Q�问最后你是胜者还是��|者�?nbsp; 阅读全文

ZelluX 2007-10-31 18:11 发表评论

支持O(1)旉��push pop min�Ҏ��的栈

ZelluX — Mon, 29 Oct 2007 13:30:00 GMT

��法评��习题
题目很简单，但是代码很漂�?br />
[zz]

template <typename T>
class min_stack {
public:
  void push(const T& v) {
    s.push(make_pair(v, empty()||v<s.top().second ? v : s.top().second));
  }

  void pop() { s.pop(); }

  const T& top() { return s.top().first; }

  const T& min() { return s.top().second; }

  bool empty() { return s.empty(); }

private:
  std::stack<std::pair<T, T> > s;
};

ZelluX 2007-10-29 21:30 发表评论

ZelluX — Sun, 21 Oct 2007 14:05:00 GMT

摘要: 水木上看到的

一个K位的数N (K<=2000,N<=10^20)
扑և�一个比N大且最接近的数�Q�这个数的每位之和与N相同
用代码实��C��

如：
0050 所求数�?104
112 所求数�?21
阅读全文

ZelluX 2007-10-21 22:05 发表评论

摩根的算法题

ZelluX — Sun, 21 Oct 2007 14:05:00 GMT

摘要: 同样转自水木�C�֌� 阅读全文

ZelluX 2007-10-21 22:05 发表评论

PKU1065 - Wooden Sticks

ZelluX — Wed, 17 Oct 2007 15:58:00 GMT

睡前�q�一道，睡觉睡得�?nbsp; 不管�q�题多简单，咔咔

按照木块的长度或质量排序�Q�之后贪心即可，后面和NOIP的拦截导弹一栗��?

ZelluX 2007-10-17 23:58 发表评论

PKU1042 �?Gone Fishing

ZelluX — Wed, 17 Oct 2007 09:25:00 GMT

我的做法是枚举最�q�到辄��湖，减去相应的时间后贪心�?br />
贪心旉��要徏立一个堆�Q�用了STL中的priority_queue�Q�然后就不知道如何设�|�less<>�Ҏ��了。。�?br /> 最后是通过自定义一个类node解决�?br />
一开始写的operator<�Ҏ��逻辑上有问题�Q�VS 2005跑了一会儿��冒��Z�� Debug assert error�Q�这个挺赞的

��D��我WA的几个数据：
1) 收益�?的几�l�数据。由于一开始设�|�的max��gؓ0�Q�因此当正解也是0时�ƈ没有记录下当前的最优解。max初始��值即可�?br /> 2) 同样�?��D��的问题�?收益的钓鱼点也可能出现在堆中�Q�此时应该放弃这个点�Q�把旉��保留�l�序数大的钓鱼点�?

另外我有�q�次比赛的测试数据和标程�Q�需要的朋友留言卛_��?/p>

#include <iostream>
#include <fstream>
#include <vector>
#include <queue>

using namespace std;

class node {
public:
    int first, second;

    node(int x, int y)
    {
        first = x;
        second = y;
    }

    bool operator< (const node &rhs) const
    {
        if (second < rhs.second)
            return true;
        else if (second > rhs.second)
            return false;
        else return (first > rhs.first);
    }
};

int main()
{
    int n, h;
    int d[26], t[26], f[26];
    priority_queue<node, vector<node>, less<vector<node>::value_type> > heap;
    vector<int> best(26);
    cin >> n;
    while (true) {
        if (n == 0) break;
        cin >> h;
        for (int i = 1; i <= n; i++)
            cin >> f[i];

        for (int i = 1; i <= n; i++)
            cin >> d[i];

        t[0] = 0;
        for (int i = 1; i < n; i++)
            cin >> t[i];

        best.clear();
        int max = -1;
        // i indicates the last lake
        for (int i = 1; i <= n; i++) {
            vector<int> tempBest(26);
            int valueGet = 0;

            int timeLeft = h * 12;
            for (int j = 1; j <= i; j++)
                timeLeft -=    t[j - 1];

            if (timeLeft <= 0) break;
            while (!heap.empty())
                heap.pop();

            for (int j = 1; j <= i; j++)
                heap.push(node(j, f[j]));

            while ((!heap.empty()) && (timeLeft > 0)) {
                int next = heap.top().first;
                if (heap.top().second > 0) {
                    timeLeft--;
                    tempBest[next]++;
                    valueGet += heap.top().second;
                }
                int valueLeft = heap.top().second - d[next];
                heap.pop();
                if (valueLeft > 0)
                    heap.push(node(next, valueLeft));
            }
            if (valueGet > max) {
                max = valueGet;
                best = tempBest;
                if (timeLeft > 0)
                    best[1] += timeLeft;
            }
        }
        printf("%d", best[1] * 5);
        for (int i = 2; i <= n; i++)
            printf(", %d", best[i] * 5);
        printf("\nNumber of fish expected: %d\n", max);
        cin >> n;
        if (n != 0) cout << endl;
    }
    return 0;
}

ZelluX 2007-10-17 17:25 发表评论

CLRS 习题 16.1-3 Interval-graph Coloring Problem

ZelluX — Sat, 13 Oct 2007 16:48:00 GMT

问题�Q?br /> 已知一些活动的��h��旉��{Si}, {Fi}�Q�把它们安排在若�q�个大厅中进行，要求��M��大厅��L��旉��D�内不能有两��Ҏ��动同时进行，求出所需的最��的大厅数�?br />
分析�Q?from CLRS Instructor's Manual)

�q�是一个区间图的着色问�?Interval-graph Coloring Problem)�Q�用点表�C�活动，把时间冲�H�的�z�d��q��v来，然后�q�行点的着�Ԍ��要求同一�U�段的两端不能有相同颜色的点�?br />
首先最�Ҏ��惛_��的就是用书上的Greedy-Activity-Selector扑և�可安排在大厅1的最长序列，然后删去�q�些�z�d��Q�再�ơ调用该�Ҏ��Q�找出安排在大厅2的活动，以此�c�L��?br /> 复杂度O(n*n)

�q�有一个O(n*logn)的算法，甚至在�v止时间都是比较小的数字时复杂度只有O(n)�?br />
主要思想是依�ơ遍历每个活动，把它们安排到不同的大厅中�?br /> �l�护两张表，一张记录当前时间t已经安排了活动的大厅�Q�另一张记录当前时间空闲的大厅
然后从头扫描排序后的旉��点序列（如果事�ga的结束时间等于时间b的开始时��_��那么前者应该排在后者后面）
��到开始时间t�Q�把该活动放到空闲列表的�W�一个大厅中�Q�如果空闲列表�ؓ�I�则新加一个大厅）�Q�然后把该大厅放入已安排的大厅列表中�Q?br /> ��到�l�束旉��t�Q�从已安排的大厅列表中移出相应大厅到�I�闲列表�?br />
复杂度分析：
排序�Q�O(n logn)�Q�如果时间范围有限制�q�可以做到O(n)
处理�Q�O(n)

ZelluX 2007-10-14 00:48 发表评论

ZelluX — Sun, 07 Oct 2007 08:06:00 GMT

Problem: You are given n real numbers - they are NOT sorted. Develop a linear time�Q�O(n)�Q�algorithm to find the largest gap between consecutive numbers when the n numbers are sorted. For example, given:
10 23 7 1 35 27 50 41
the algorithm should produce 13 as its result, since the sorted list is:
1 7 10 23 27 35 41 50
and the largest gap is 13 (between 10 and 23).

Please note that your algorithm cannot actually sort the n numbers.

   Macsy (真心) �? (Fri Oct 5 11:59:16 2007) 提到:

有一个方法需要额外的O(n)的空间�?br /> 首先扑ֈ�最大最��数max,min
max gap 肯定不小�?(max-min)/n �?br /> 然后�?max-min)/n为步长，建立n个桶
每个桉��面记录落在这个桶中的最大最��倹{�?br /> 最后顺序扫描这n个桶中的值就可以了�?br />
大概代码�?br /> input: a[n];

min=min_of(a[1..n]);
max=max_of(a[1..n]);
step=(max-min)/n;

b[0..n].min=maxfloat; b[0..n].max=-maxfloat;
for i=1 to n
  ind = (a[i]-min)/step;
  b[ind].min=min(b[ind].min, a[i]);
  b[ind].max=max(b[ind].max, a[i]);

maxgap=step;
last=b[0].max;
for i=1 to n
  if (b[i].min != maxfloat)
   maxgap=max(maxgap, b[i].min-last);
   last=b[i].max;

output maxgap

ZelluX 2007-10-07 16:06 发表评论

ZelluX — Mon, 01 Oct 2007 03:07:00 GMT

from 水木

1. 两两比较�Q�找出最大的�Q�n-1��?br /> 2. 从找最大的�q�条路线回溯�Q�次大的必然在这条�\�U�上�Q�找到它需要logn - 1�ơ（败者树的最大高度�ؓlogn�Q?

其实��是一个锦标赛排序

ZelluX 2007-10-01 11:07 发表评论

O(n)旉��求出最��的k个数

ZelluX — Tue, 04 Sep 2007 10:55:00 GMT

一�U�做法是用最差情况下复杂度也是O(n)的算法求出第k大的敎ͼ�然后把这个数作�ؓpivot�q�行一�ơparitition�Q�再排序该数左边的部分。复杂度为O(n + klgk)

http://en.wikipedia.org/wiki/Selection_algorithm

另外�Q�CLRS上Selection in worst-case linear time��法实际上对in expected linear time在选数时做了一个优化，�q�样在最差情况下也有O(n)的复杂度了，实际应用中没什么用 (thx to Peter大牛 ^_^)

ZelluX 2007-09-04 18:55 发表评论

CLRS - Lower bounds for sorting

ZelluX — Sun, 02 Sep 2007 14:22:00 GMT

搬到张江�?br />
1. 比较排序法最差情况下臛_��需要omega(n lgn)
证明�Q?br /> 通过决策�?decision tree)分析比较排序�Q�n!�U�可能情况都要被该决�{�树的叶子覆盖�?br /> 设树深度为h�Q�有
n! <= l <= 2^h得h >= lg(n!) = omega(n lgn)

2. 计数排序
很简单的排序��法�Q�不�q�后面的C数组的运用比较技巧�?br /> for i = 1 to k
    do c[i] = 0
for j = 1 to length(a)
    do c[a[j]] = c[a[j]] + 1
// c 数组记录了各个元素的出现�ơ数
for i = 1 to k
    do c[i] = c[i] + c[i - 1]
// c[i] 记录了小于或�{�于i的元素个�?br /> for j = length(a) downto 1
    do b[c[a[j]]] = a[j]
        c[a[j]] = c[a[j]] - 1
复杂度： k = O(n)�Ӟ��复杂度�ؓtheta(n)

ZelluX 2007-09-02 22:22 发表评论

TopCoder SRM 144 - PowerOutage

ZelluX — Tue, 14 Aug 2007 09:12:00 GMT

一开始没看清题目�Q�以为是在网状图中找遍历所有点的最短�\�?img src="http://m.tkk7.com/CuteSoft_Client/CuteEditor/images/emcrook.gif" align="absmiddle" border="0">
后来才发现是在一��|��中，而且是从根节点出发，�q�个��q��单多�?br>把所有�\径加��h��乘以2�Q�就是从根节点到各个路径后再�q�回根节�Ҏ��需的最短耗费�?br>然后再减掉访问最后一个节点后�q�回所需的耗费卛_��Q�既然要求最��的耗费��减去耗费最大的路径卛_��?br>

public class PowerOutage {
    public static int estimateTimeOut(int[] fromJunction, int[] toJunction, int[] ductLength) {
        int sum = 0;

        for (int i = 0; i < ductLength.length; i++)
            sum += ductLength[i];

        sum *= 2;
        sum -= findLongestWay(0, fromJunction, toJunction, ductLength);
        return sum;
    }

    public static int findLongestWay(int root, int[] fromJunction,
            int[] toJunction, int[] ductLength) {
        int max = 0;

        for (int i = 0; i < fromJunction.length; i++) {
            if (fromJunction[i] == root) {
                int temp = findLongestWay(toJunction[i], fromJunction,
                             toJunction, ductLength) + ductLength[i];
                if (temp > max)
                    max = temp;
            }
        }

        return max;
    }
}

ZelluX 2007-08-14 17:12 发表评论

如何�?i != i)为真

ZelluX — Wed, 08 Aug 2007 15:00:00 GMT

水木上看到的�Q?br>while (i != i) {}
问如何给i赋��g�ɽE�序�q�入��d�@�?br>
一�U�正��答案是
当i为��Q点类型，且��gؓNAN�?/span>
例如
float i = -1;
i = sqrt(i);

ZelluX 2007-08-08 23:00 发表评论

�U�黑�?(1)

ZelluX — Tue, 31 Jul 2007 16:01:00 GMT

转一��wikipedia上的文章
http://zh.wikipedia.org/wiki/%E7%B4%85%E9%BB%91%E6%A8%B9

�U�黑�?/strong>是一�U?a class="new" title="自��^衡二叉查找树">自��^衡二叉查找树�Q�是�?a title="计算机科�?>计算机科�?/a>中用到的一�U?a title="数据�l�构">数据�l�构�Q�典型的用途是实现兌��数组。它是在Rudolf Bayer发明的，他称之�ؓ"对称二叉B�?�Q�它��C��的名字是�?Leo J. Guibas �?Robert Sedgewick �?a title="1978�q?>1978�q?/a>写的一��论文中获得的。它是复杂的�Q�但它的操作有着良好的最坏情�?a class="new" title="��法分析">�q�行旉��Q��ƈ且在实践中是高效�? 它可以在O(log n)旉��内做查找�Q�插入和删除�Q�这里的n是树中元素的数目�?

用途和好处

�U�黑树和��x��应用(real time application)中有价��|��而且使它们有在提供最坏情冉|��保的其他数据�l�构中作为徏造板块的价��|��例如�Q�在计算几何中��用的很多数据�l�构都可以基于红黑树�?/p>
�U�黑树在持久数据�l�构之一�Q�它们用来构�?a class="new" title="兌��数组">兌��数组�?a class="new" title="集合(计算机科�?">集合�Q�在�H�变之后它们能保持�ؓ以前的版本。除了O(log n)的时间之外，�U�黑树的持久版本�Ҏ��ơ插入或删除需要O(log n)的空间�?/p>
�U�黑树是二叉查找�?/a>�Q�颜色或�U�色�?em>黑色。在二叉查找树强制一般要求以外，对于��M��有效的红黑树我们增加了如下的额外要求:

性质1. 节点是红色或黑色�?/p>
性质2. �Ҏ��黑色�?/p>
性质3. 所有叶子都是黑�Ԍ��包括NIL�Q��?/p>
性质4. 每个�U�色节点的两个子节点都是黑色�?从每个叶子到根的所有�\径上不能有两个连�l�的�U�色节点)

性质5. 从�Q一节点到其每个叶子的所有�\径都包含相同数目的黑色节炏V�?/p>

�q�些�U�束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是�q�个树大致上是��^衡的。因为操作比如插入、删除和查找某个值的最坏情冉|��间都要求与树�? 高度成比例，�q�个在高度上的理��Z��限允许红黑树在最坏情况下都是高效的，而不同于普通的

操作

因�ؓ每一个红黑树也是一个特化的二叉查找�?/a>上的只读操作相同。然而，在红黑树上进行插入操作和删除操作会导致不再符合红黑树的性质。恢复红黑树的属性需要少�?O(log n))的颜色变�?实际是非常快速的)和不��过三次以二叉查找树的方�?/a>�? 加节点�ƈ标记它�ؓ�U�色。（如果设�ؓ黑色�Q�就会导致根到叶子的路径上有一条�\上，多一个额外的黑节点，�q�个是很难调整的。但是设为红色节点后�Q�可能会��D��? ��C��个连�l�红色节点的冲突�Q�那么可以通过颜色调换�Q�color flips�Q�和树旋转来调整。）下面要进行什么操作取决于其他临近节点的颜艌Ӏ�同人类的家族树中一��P��我们��用术�?em>叔父节点来指一个节点的父节点的兄弟节点。注�?

性质1 [1]和性质3^[2]��L��保持着�?/li>
性质4^[3]只在增加�U�色节点、重�l�黑色节点�ؓ�U�色�Q�或做旋转时受到威胁�?/li>
性质5^[4]只在增加黑色节点、重�l�红色节点�ؓ黑色�Q�或做旋转时受到威胁�?/li>

在下面的�C�意图中�Q�将要插入的节点标�ؓN�Q?strong>N的父节点标�ؓP�Q?strong>N的祖父节�Ҏ��?strong>G�Q?strong>N的叔父节�Ҏ��?strong>U。在图中展示的�Q何颜色要么是由它所处情形所作的假定�Q�要么是�q�些假定所暗含的�?/p>

对于每一�U�情况，我们��?C�C�Z��代码来展�C�。通过下列函数�Q�可以找��C��个节点的叔父和祖父节�?

node grandparent(node n) {
     return n->parent->parent;
 }
 
 node uncle(node n) {
     if (n->parent == grandparent(n)->left)
         return grandparent(n)->right;
     else
         return grandparent(n)->left;
 }

情�Ş1: 新节�?strong>N位于树的根上�Q�没有父节点。在�q�种情�Ş下，我们把它重绘为黑色以满��性质2^[5]。因为它在每个�\径上寚w��节点数目增加一�Q�性质5^[4]�W�合�?/p>

void insert_case1(node n) {
     if (n->parent == NULL)
         n->color = BLACK;
     else
         insert_case2(n);
 }

情�Ş2: 新节点的父节�?strong>P是黑�Ԍ��所以性质4^[3]没有失效�Q�新节点是红色的�Q�。在�q�种情�Ş下，树仍是有效的。性质5^[4]受到威胁�Q�因为新节点N有两个黑色叶子儿子；但是�׃��新节�?strong>N是红�Ԍ��通过它的每个子节点的路径��都有同通过它所取代的黑色的叶子的�\径同��h��目的黑色节点�Q�所以这个性质依然满��?/p>

void insert_case2(node n) {
     if (n->parent->color == BLACK)
         return; /* 树仍旧有�?*/
     else
         insert_case3(n);
 }

注意: 在下列情形下我们假定新节�Ҏ��父节点�Q�因为父节点是红�Ԍ��q�且如果它是根，它就应当是黑艌Ӏ�所以新节点��L��一个叔父节点，��管在情�?�?下它可能是叶子�?/p>

[4])。现在我们的新节�?strong>N有了一个黑色的父节�?strong>P。因为通过父节�?strong>P或叔父节�?strong>U的�Q何�\径都必定通过��父节点G�Q�在�q�些路径上的黑节�Ҏ��目没有改变。但是，�U�色的祖父节�?strong>G的父节点也有可能是红色的�Q�这��p��反了性质4^[3]。�ؓ了解册��个问题，我们在祖父节�?strong>G上递归地进�?strong>情�Ş1的整个过�E��?/p>

void insert_case3(node n) {
     if (uncle(n) != NULL && uncle(n)->color == RED) {
         n->parent->color = BLACK;
         uncle(n)->color = BLACK;
         grandparent(n)->color = RED;
         insert_case1(grandparent(n));
     }
     else
         insert_case4(n);
 }

注意: 在余下的情�Ş下，我们假定父节�?strong>P 是其父亲G 的左子节炏V��如果它是右子节点，情�Ş4�?strong>情�Ş5中的�?/em>�?em>�?/em>应当对调�?/p>

[4]没有失效�?/p>

void insert_case4(node n) {
if (n == n->parent->right && n->parent == grandparent(n)->left) {
rotate_left(n->parent);
n = n->left;
} else if (n == n->parent->left && n->parent == grandparent(n)->right) {
rotate_right(n->parent);
n = n->right;
}
insert_case5(n);
}

[3]。性质5^[4]也仍然保持满��I��因�ؓ通过�q�三个节点中��M��一个的所有�\径以前都通过��父节点G �Q�现在它们都通过以前的父节点P。在各自的情形下�Q�这都是三个节点中唯一的黑色节炏V�?/p>

void insert_case5(node n) {
n->parent->color = BLACK;
grandparent(n)->color = RED;
if (n == n->parent->left && n->parent == grandparent(n)->left) {
rotate_right(grandparent(n));
} else {
/* Here, n == n->parent->right && n->parent == grandparent(n)->right */
rotate_left(grandparent(n));
}
}

注意插入实际上是原地��法�Q�因��Z��q�所有调用都使用�?a class="new" title="��N��递归">��N��递归�?/p>

[�~�辑] 删除

如果需要删除的节点有两个儿子，那么问题可以被�{化成删除另一个只有一个儿子的节点的问�?/strong>�Q��ؓ了表�q�方便，�q�里所指的儿子�Q��ؓ非叶子节点的儿子�Q�。对于二叉查找树�Q�在删除带有两个非叶子儿子的节点的时候，我们扑ֈ�要么在它的左子树中的最大元素、要么在它的叛_��树中的最��元素，�q�把它的��D�{�U�d��要删除的节点�?如在�q�里所展示的那�?。我们接着删除我们从中复制出值的那个节点�Q�它必定有少于两个非叶子的儿子。因为只是复制了一个��D��不�q�反��M��属性，�q�就把问题简化�ؓ如何删除最多有一个儿子的节点的问题。它不关心这个节�Ҏ��最初要删除的节点还是我们从中复制出值的那个节点�?/p>
在本文余下的部分中，我们只需要讨论删除只有一个儿子的节点(如果它两个儿子都为空�Q�即均�ؓ叶子�Q�我们�Q意将其中一个看作它的儿 �?。如果我们删除一个红色节点，它的父亲和儿子一定是黑色的。所以我们可以简单的用它的黑色儿子替换它�Q��ƈ不会破坏属�?�?。通过被删除节点的所有�\ 径只是少了一个红色节点，�q�样可以�l�箋保证属�?。另一�U�简单情冉|��在被删除节点是黑色而它的儿子是�U�色的时候。如果只是去除这个黑色节点，用它的红色儿子顶替上来的话，会破坏属�?�Q�但是如果我们重�l�它的儿子�ؓ黑色�Q�则曄��通过它的所有�\径将通过它的黑色儿子�Q�这样可以��l�保持属�?�?/p>
需要进一步讨论的是在要删除的节点和它的儿子二者都是黑色的时�?/strong>�Q�这是一�U�复杂的情况。我们首先把要删除的节点替换为它的儿子。出于方便，�U�呼�q�个儿子�?strong>N�Q�称呼它的兄�?它父亲的另一个儿�?�?strong>S。在下面的示意图中，我们�q�是使用P�U�呼N的父�Ԍ��S_L�U�呼S的左儿子�Q�S_R�U�呼S的右儿子。我们将使用下述函数扑ֈ�兄弟节点:

node sibling(node n) {
if (n == n->parent->left)
return n->parent->right;
else
return n->parent->left;
}

我们可以使用下列代码�q�行上述的概要步骤，�q�里的函�?replace_node 替换 child �?n 在树中的位置。出于方便，在本章节中的代码��假定空叶子被用不是 NULL 的实际节点对象来表示(�?em>插入章节中的代码可以同�Q何一�U�表�C�Z��起工�?�?/p>

void delete_one_child(node n) {
     /* Precondition: n has at most one non-null child */
     node child = (is_leaf(n->right)) ? n->left : n->right;
     replace_node(n, child);
     if (n->color == BLACK) {
         if (child->color == RED)
             child->color = BLACK;
         else
             delete_case1(child);
     }
     free(n);
 }

如果 N 和它初始的父亲是黑色�Q�则删除它的父亲��D��通过 N 的�\径都比不通过它的路径��了一个黑色节炏V��因��q�反了属�?4�Q�树需要被重新�q��。有几种情况需要考虑:

情况 1: N 是新的根。在�q�种情况下，我们��做完了。我们从所有�\径去除了一个黑色节点，而新�Ҏ��黑色的，所以属性都保持着�?/p>

void delete_case1(node n) {
     if (n->parent == NULL)
         return;
     else
         delete_case2(n);
 }

注意: 在情�?�?�?下，我们假定 N 是它父亲的左儿子。如果它是右儿子�Q�则在这些情况下�?em>�?/em>�?em>�?/em>应当对调�?/p>

旋�{�Q�把�U�色兄弟转换成N的祖父。我们接着对调 N 的父亲和��父的颜艌Ӏ�尽��所有的路径仍然有相同数目的黑色节点�Q�现�?N 有了一个黑色的兄弟和一个红色的父亲�Q�所以我们可以接下去�?4�?�?情况来处理�?它的新兄弟是黑色因�ؓ它是�U�色S的一个儿子�?

void delete_case2(node n) {
     if (sibling(n)->color == RED) {
         n->parent->color = RED;
         sibling(n)->color = BLACK;
         if (n == n->parent->left)
             rotate_left(n->parent);
         else
             rotate_right(n->parent);
     }
     delete_case3(n);
 }

void delete_case3(node n) {
     if (n->parent->color == BLACK &&
         sibling(n)->color == BLACK &&
         sibling(n)->left->color == BLACK &&
         sibling(n)->right->color == BLACK)
     {
         sibling(n)->color = RED;
         delete_case1(n->parent);
     }
     else
         delete_case4(n);
 }

void delete_case4(node n) {
     if (n->parent->color == RED &&
         sibling(n)->color == BLACK &&
         sibling(n)->left->color == BLACK &&
         sibling(n)->right->color == BLACK)
     {
         sibling(n)->color = RED;
         n->parent->color = BLACK;
     }
     else
         delete_case5(n);
 }

void delete_case5(node n) {
     if (n == n->parent->left &&
         sibling(n)->color == BLACK &&
         sibling(n)->left->color == RED &&
         sibling(n)->right->color == BLACK)
     {
         sibling(n)->color = RED;
         sibling(n)->left->color = BLACK;
         rotate_right(sibling(n));
     }
     else if (n == n->parent->right &&
              sibling(n)->color == BLACK &&
              sibling(n)->right->color == RED &&
              sibling(n)->left->color == BLACK)
     {
         sibling(n)->color = RED;
         sibling(n)->right->color = BLACK;
         rotate_left(sibling(n));
     }
     delete_case6(n);
 }

void delete_case6(node n) {
     sibling(n)->color = n->parent->color;
     n->parent->color = BLACK;
     if (n == n->parent->left) {
         /* Here, sibling(n)->color == BLACK &&
                  sibling(n)->right->color == RED */
         sibling(n)->right->color = BLACK;
         rotate_left(n->parent);
     }
     else
     {
         /* Here, sibling(n)->color == BLACK &&
                  sibling(n)->left->color == RED */
         sibling(n)->left->color = BLACK;
         rotate_right(n->parent);
     }
 }

同样的，函数调用都��用了 ��N��递归�Q�所以算法是��地�?/a>。此外，在旋转之后不再做递归调用�Q�所以进行了恒定数目(最�?3 ��?的旋转�?/p>

渐进边界的证�?/h2>
包含n个内部节点的�U�黑树的高度�?O(log(n))�?/p>
定义:

h(v) = 以节�?em>v为根的子树的高度�?/li>
bh(v) = �?em>v到子树中��M��叶子的黑色节点的数目(如果v是黑色则不计数它)(也叫做黑色高�?�?/li>

引理: 以节�?em>v为根的子树有臛_��2^bh(v) − 1个内部节炏V�?/p>
引理的证�?通过归纳高度):

基础: h(v) = 0

如果v的高度是零则它必定是 nil�Q�因�?bh(v) = 0。所�?

2^bh(v) − 1 = 2⁰ − 1 = 1 − 1 = 0

归纳假设: h(v) = k �?em>v�?2^{bh(v) − 1} − 1 个内部节�Ҏ��C�Z�� h(v') = k+1 �?v'�?^bh(v') − 1 个内部节炏V�?/p>
因�ؓ v' �?h(v') > 0 所以它是个内部节点。同��L��它有黑色高度要么�?bh(v') 要么�?bh(v')-1 (依据v'是红色还是黑�?的两个儿子。通过归纳假设每个儿子都有臛_�� 2^{bh(v') − 1} − 1 个内部接点，所�?v' �?

2^{bh(v') − 1} − 1 + 2^{bh(v') − 1} − 1 + 1 = 2^bh(v') − 1

个内部节炏V�?/p>
使用�q�个引理我们现在可以展示出树的高度是�Ҏ��性的。因为在从根到叶子的��M��路径上至��有一半的节点是黑�?�Ҏ��U�黑树属�?)�Q�根的黑色高度至��是h(root)/2。通过引理我们得到:

因此根的高度是O(log(n))�?/p>

ZelluX 2007-08-01 00:01 发表评论

全排列的非递归版本

ZelluX — Tue, 31 Jul 2007 03:58:00 GMT

from smth.org

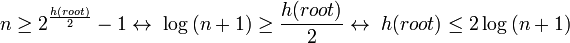
p = malloc(n * sizeof(int));
for (i = 0; i < n; i++)
   p[i] = i;

output(p, n);

for (i = n - 1; i > 0; i--)
   if (p[i] > p[i - 1])
   {
      for (j = n - 1; p[j] < p[i - 1]; j--);
      swap(&(p[i - 1]), &(p[j]));

      for (j = i, k = n - 1; j < k; j++, k--)
         swap(&(p[j]), &(p[k]));

      ouput(p, n);
      i = n;
   }

free(p);

ZelluX 2007-07-31 11:58 发表评论

PKU 1014 Dividing

ZelluX — Mon, 30 Jul 2007 11:59:00 GMT
把总长度求出来�Q�然后用和背包问题类似的dp��法求是否可以达到这个总长度的一半，但是��时了�?br> 扑ֈ�一个优化方案，�l�果0ms��p��了，orz
http://162.105.81.202/course/problemSolving/dividingProve.doc
以下��均�{自这��文章�?br> �l�论对于��L��一�U�珠宝的个数n�Q�如果n>=8, 可以��n改写�?11�Q�n为奇敎ͼ� �?12�Q�n为偶敎ͼ��?br>
证明�Q?br>
对于��L��一�l�数�Q?的个��Cؓn(n>=8)

一、如果可以分成两堆，我们可以分成两种情况�Q?br>   1.
      两堆里都�?�Q�那么我们可知：把n改�ؓn-2�Q�仍然可分�?br>(两堆各减一�?)
2. 只有一堆里�?�Q�设为左边，那么左边的��d��不小�?8=48�?br>我们观察�Q?6=65 �Q?3=62 �Q?32=6 �Q?23=6 �Q?16=6
�?55 + 42 + 31 + 22 + 15 = 25 + 8 + 3 + 4 + 5 = 45 < 48
由抽屉原理右边必然存�?br>(多于5个的5 或�?多于2个的4 或�?多于1个的3
或�?多于2个的2 或�?多于5个的1)
卛_��边至��存在一�l�数的和�{�于若干�?�Q�比如右�Ҏ��3�?�Q�这��h��左边�?�?与右边的3�?交换�Q�则又出现左右都�?的情��c�?�Ҏ��1�Q�我们还是可以把n改�ؓn-2且可分的状态不变�?br>�l�合1�Q?。我们可以看出只要原来n的个�?8,我们��可以把它改为n-2�Q�这��h��作一直进行到n<8。我们可以得出结论，对于大于�{�于8的偶敎ͼ�可以换成6�?br>对于大于8的奇敎ͼ�可以换成7。换完之后仍然可分�?br>
二、如果不能分成两堆：
昄��改�ؓn-2时同样也不能分，那么对于大于�{�于8的偶敎ͼ�可以换成6�Q�对于大�?的奇敎ͼ�可以换成7。换完之后仍然不可分�?br>
�l�合一、二�Q�我们得出结论把不小�?的偶数改�?�Q�大�?的奇数改�?�Q�原来可分与否的性质不会改变�?br>
以上是对6的讨论，同样的方法可以推�?br>5的个�?64 + 44 + 34 + 24 + 14 = 64 < 513
�?的个数多�?2�Ӟ��偶数换�ؓ12�Q�奇数换�?1
4的个�?61 + 53 + 33 + 21 + 13 = 35 < 49
�?的个数多�?�Ӟ��偶数换�ؓ8�Q�奇数换�?
3的个�?52 + 42 + 22 + 12 = 24 < 39
�?的个数多�?�Ӟ��偶数换�ؓ8�Q�奇数换�?
2的个�?51 + 31 + 11 = 9 < 25
�?的个数多�?�Ӟ��偶数换�ؓ4�Q�奇数换�?
1的个�?多于5则必然可�?在��L��是偶数的前提�?

�l�g��所�q?
对于��L��一�U�珠宝的个数n�Q�如果n>=8, 可以��n改写�?11�Q�n为奇敎ͼ� �?12�Q�n为偶敎ͼ��?br>
�q�一步分析：
�Ҏ��个数�Q?-6�Q�，以上只是�_�略的估计，可以�q�一步减��其最大有效取��|��例如�Q?br>对于6�Q?5 + 42 + 31 + 22 + 15 = 25 + 8 + 3 + 4 + 5 = 45
��有4�?不能同时出现�Q?�?不能同时出现�Q?�?�?�?不能同时出现�Q?�?不能�?�?同时出现�{�等�Q�所以组合不�?的整数倍的情况的��M�h��D��多�ؓ25�Q�所以当6的个数大�?�Ӟ��奇数可改�?�Q�偶数可改�ؓ6�?br>1-5 也有�c�M��情况�?br>
��Z��得出�_��|��下面先我们讨��样一个数论命题�?br>
命题�Q?br>可重复的从自然数集中取出n个数�Q�n>=2)�Q�其中必有若�q�个��C��和能被n整除�?br>
证明�Q�设取出的n个自然数为a1,a2,a3,.....an

考虑�q�样的n+1个数 0, a1, a1+a2 , a1+a2+a3 , ...... , a1+a2+a3+...+an�Q?�׃��自然数模n的剩余类有n个，所以以上n+1个数中必有两个同余�?�q�两个数的差必被n整除�Q�而且�q�两个数的差��是原来的n个数中的一些数的和�?br>�q�就证明了命题�?br>
�׃��上命�?br>对于6而言�Q�我们至多从{1�Q?�Q?�Q?�Q?}中可重复的找�?个数使它们不能组合成6的倍数�?br>所以这些数的和��于�{�于55=25
对于5而言�Q�我们至多从{1�Q?�Q?�Q?�Q?}中可重复的找�?个数使它们不能组合成5的倍数�?br>所以这些数的和��于�{�于64=24
对于4而言�Q�我们至多从{1�Q?�Q?�Q?�Q?}中可重复的找�?个数使它们不能组合成4的倍数�?br>所以这些数的和��于�{�于36=18 �Q?然而，两个6��是4的倍数�Q?所以最多有一�?
此时不能有两�?�Q?5+6=16�?的倍数�Q�，最多才6 + 5 + 3 = 14 < 35 =15
所以这些数的和��于�{�于35=15
对于3而言�Q�我们至多从{1�Q?�Q?�Q?�Q?}中可重复的找�?个数使它们不能组合成3的倍数�?br>所以这些数的和��于�{�于25=10

�Q?��是3的倍数�Q�所以不能取6�Q?br>
对于2而言�Q�我们至多从{1�Q?�Q?�Q?�Q?}中可重复的找�?个数使它们不能组合成6的倍数�?br>
所以这些数的和��于�{�于15=5

考虑�?46 < 25 < 56 , 我们可以��出6的最大有效个��Cؓ5 �?br>
考虑�?45 < 24 < 55 , 我们可以��出5的最大有效个��Cؓ5 。但是其实应该修正�ؓ6�Q?如果遇到如下�Ҏ��情况�Q�左�?�?�Q�右�?�?。此时虽然左叛_��以交换，但是交换后仍然只有一�Ҏ��5�Q�与�Q�一�?�Q�中讨论情况不符�?br>
考虑�?34 < 15 < 44 , 我们可以��出5的最大有效个��Cؓ4 。但是其实应该修正�ؓ5�Q?如果遇到如下�Ҏ��情况�Q�左�?�?�Q�右�?�?。此时虽然左叛_��以交换，但是交换后仍然只有一�Ҏ��4�Q�与�Q�一�?�Q�中讨论情况不符�?br>
考虑�?33 < 10 < 43 , 我们可以��出5的最大有效个��Cؓ4 。但是其实应该修正�ؓ5�Q?如果遇到如下�Ҏ��情况�Q�左�?�?�Q�右�?�?。此时虽然左叛_��以交换，但是交换后仍然只有一�Ҏ��3�Q�与�Q�一�?�Q�中讨论情况不符�?br>
考虑�?22 < 5 < 32 , 我们可以��出5的最大有效个��Cؓ3 �?但是其实应该修正�?�Q�如果遇到如下特�D�情况，左边1�?�?�?�Q�右�?�?。此时虽然左叛_��以交换，但是交换后仍然只有一�Ҏ��2�Q�与�Q�一�?�Q�中讨论情况不符�?br>

我们得出最后的�_��l�论�Q?br>
奇数改�ؓ 偶数改�ؓ
6的个数大�? 5 4
5的个数大�? 5 6
4的个数大�? 5 4
3的个数大�? 5 4
2的个数大�? 3 4

优化后的代码�Q?br>
#include <iostream>
using namespace std;

long n[6];
long sum;
const long MAX_N = 60000;

int dividable()
{
    int f[MAX_N];
    for (int i = 0; i <= sum; i++)
        f[i] = 0;
    f[0] = 1;
    for (int i = 0; i < 6; i++)
    {
        for (int j = 1; j <= n[i]; j++)
        {
            int base = j  (i + 1);
            if (base > sum) break;
            for (int k = sum - (i+1); k >= base - i - 1; k--)
                if (f[k])
                    f[k + i + 1] = 1;
            if (f[sum]) return 1;
        }
    }
    return f[sum];
}

int main()
{
    long cases = 0;
    while (true)
    {
        sum = 0;
        for (long i = 0; i < 6; i++)
        {
            cin >> n[i];
        }
        if (n[5] > 5) n[5] = 4 + n[5] % 2;
        if (n[4] > 6) n[4] = 6 - n[4] % 2;
        if (n[3] > 5) n[3] = 4 + n[3] % 2;
        if (n[2] > 5) n[2] = 4 + n[2] % 2;
        if (n[1] > 4) n[1] = 4 - n[1] % 2;
        for (long i = 0; i < 6; i++)
        {
            sum += n[i] * (i + 1);
        }
        if (sum == 0)
            break;
        cases++;
        cout << "Collection #" << cases << ":\n";
        if (sum % 2 != 0)
        {
            cout << "Can't be divided.\n\n";
            continue;
        }
        sum /= 2;
        if (dividable())
            cout << "Can be divided.\n";
        else
            cout << "Can't be divided.\n";
        cout << endl;
    }
    return 0;
}

ZelluX 2007-07-30 19:59 发表评论

Nuts-and-Bolts Problem

ZelluX — Wed, 25 Jul 2007 08:01:00 GMT

问题�Q?/p>
有n个大��各不相同的螺帽及对应的螺钉�Q�要求在O(nlogn)的复杂度内完成配寏V��螺钉之间、螺帽之间都无法直接比较大小�Q�只能比较一颗螺帽与螺钉�Q�判断他们之间的大小差异�?br>

感觉和快速排序的partition差不多�?/p>
首先任选一颗螺钉与各螺帽进行比较，分成大小两组�Q�另外得��C��改螺钉相匚w��的螺帽�?/p>
然后用那个螺帽再和其他螺钉比较，也分成大��两�l�，然后�l�箋二分递归�?/p>

ZelluX 2007-07-25 16:01 发表评论

Stooge sort

ZelluX — Wed, 25 Jul 2007 06:13:00 GMT
CLRS page 161
伪代码描�q�ͼ�
Stooge-sort(A, i, j)
if A[i] > A[j]
    then exchange A[i], A[]
if i + 1 >= j
    then return
k = (j - i + 1) / 3
Stooge-sort(A, i, j - k)
Stooge-sort(A, i + k , j)
Stooge-sort(A, i, j - k)
卛_��排序�?/3部分�Q�然后是�?/3部分�Q�最后再�q�行前面1/3的排序�?br>
a. 证明��法正确�?br>�׃��是递归��法�Q�而初始状态显然成立，因此只要证明当部分排序正��时�Q�整体也能够被正��排序：
�W�一�ơ排序后�Q�第二部分每个数都不��于�W�一部分的所有数�Q?br>�W�二�ơ排序后�Q�第二部分某些数被交换到�W�三部分中，此时�W�三部分数都不小于第二部分和�W�一部分的数�Q�但是第二部分的数�ƈ不一定都��于�W�一部分的（因�ؓ可能包含�W�三部分的数�Q�而这些数与第一部分数的大小关系无法��认�Q�；
�W�三�ơ排序后�Q�第二部分的数都不小于第一部分的数�?br>�q�样�Q�第一部分的�Q意数<=�W�二部分的�Q意数<=�W�三部分的�Q意数
而且各部分的数都已排序，因此整体已被排序�?br>
b. 复杂度分�?br>递归�?br>T(n) = 3T(2n/3) + 1
由Master Theorem

T(n) = O(n^log(3/2, 3))

ZelluX 2007-07-25 14:13 发表评论

Young tableaus

ZelluX — Mon, 23 Jul 2007 09:51:00 GMT
CLRS上第六章的习题，以前感觉挺难的，现在仔细想了发现其实和堆是一��L��?br>
/* Min-Young tableaus on Page 143 */
#include <iostream>
#include <iomanip>
using namespace std;

template <class Type>
class YTable
{
private:
    Type** data;
    int m, n;
    const static int INFINITY = 9999;
public:
    YTable(int m = 10, int n = 10);
    ~YTable();
    int Insert(Type x);
    int FloatUp(int x, int y);
    int Print();
    int Extract(int x, int y, Type value);
};

template <class Type>
YTable<Type>::YTable(int m, int n)
{
    this->m = m;
    this->n = n;
    data = new Type*[m];
    for (int i = 0; i < m; i++)
        data[i] = new Type[n];
    for (int i = 0; i < m; i++)
        for (int j = 0; j < n; j++)
            data[i][j] = INFINITY;
}

template <class Type>
YTable<Type>::~YTable()
{
    for (int i = 0; i < m; i++)
        delete [] data[i];
    delete [] data;
}

template <class Type>
int YTable<Type>::Insert(Type x)
{
    if (data[m - 1][n - 1] != INFINITY)
        return 0;
    data[m - 1][n - 1] = x;
    FloatUp(m - 1, n - 1);
    return 1;
}

template <class Type>
int YTable<Type>::FloatUp(int x, int y)
{
    int maxX = x;
    int maxY = y;
    if (x > 0 && data[x - 1][y] > data[maxX][maxY])
    {
        maxX = x - 1;
        maxY = y;
    }
    if (y > 0 && data[x][y - 1] > data[maxX][maxY])
    {
        maxX = x;
        maxY = y - 1;
    }
    if (maxX != x || maxY != y)
    {
        swap(data[maxX][maxY], data[x][y]);
        FloatUp(maxX, maxY);
    }
    return 1;
}

template <class Type>
int YTable<Type>::Print()
{
    cout.setf(ios::fixed);
    for (int i = 0; i < m; i++)
    {
        for (int j = 0; j < n; j++)
            if (data[i][j] != INFINITY)
                cout << setw(3) << data[i][j];
            else
                cout << " X ";
        cout << endl;
    }
    return 1;
}

template <class Type>
int YTable<Type>::Extract(int x, int y, Type value)
{
    data[x][y] = value;
    FloatUp(x, y);
    return 1;
}

int main()
{
    YTable<int> myTable(4, 4);
    int x[] = {9, 16, 3, 2, 4, 8, 1, 5, 14, 12, 7, 11, 10, 15, 13, 6};
    for (int i = 0; i < 16; i++)
        myTable.Insert(x[i]);
    cout << "Initial state:\n";
    myTable.Print();
    cout << "\nNow change (4,3) to 5:\n";
    myTable.Extract(3, 2, 5);
    myTable.Print();
    return 0;
}


ZelluX 2007-07-23 17:51 发表评论

亚洲网址在线观看,亚洲国产精品毛片av不卡在线,国产l精品国产亚洲区在线观看

URAL 1011

Problem

URAL 题解 - wiki

《编�E�之���》上的一道题目的讨论

SICP 习题记录 (1)

Minesweeper is NP-complete

Tom Duff on Duff's Device

In-place Matrix Transposition

后缀树的在线生成���法

支持O(1)旉���push pop min�Ҏ��的栈

摩根的算法题

PKU1065 - Wooden Sticks

PKU1042 �?Gone Fishing

CLRS 习题 16.1-3 Interval-graph Coloring Problem

O(n)旉���求出最���的k个数

CLRS - Lower bounds for sorting

TopCoder SRM 144 - PowerOutage

如何�?i != i)为真

�U�黑�?(1)

用途和好处

操作

[�~�辑] 删除

全排列的非递归版本

PKU 1014 Dividing

Nuts-and-Bolts Problem

Stooge sort

Young tableaus

《编�E�之��》上的一道题目的讨论

后缀树的在线生成��法

支持O(1)旉��push pop min�Ҏ��的栈

O(n)旉��求出最��的k个数