Exponentiating by squaring is an algorithm used for the fast computation of large integer powers of a number. It is also known as the square-and-multiply algorithm or binary exponentiation. In additive groups the appropriate name is double-and-add algorithm. It implicitly uses the binary expansion of the exponent. It is of quite general use, for example in modular arithmetic.
еҸ‘дҝЎдә? flyskyf (flysky), дҝЎеҢә: Algorithm
ж ? йў? жӢҝзі–жһңй—®йў?br /> еҸ‘дҝЎз«? ж°ҙжңЁҪC‘ЦҢә (Mon Oct 15 19:07:51 2007), з«ҷеҶ…
зҺ°жңү4е Ҷзі–жһ?еҲҶеҲ«дё?,2,4,8
з”Ід№ҷдёӨдқhеҲҶеҲ«д»ҺдёӯжӢҝзі–жһ?br />
规еҲҷ:
1 жҜҸдқhеҸҜд»Ҙд»ҺжҹҗдёҖе ҶдёӯжӢҝд“Qж„ҸеӨҡдё?br /> 2 з”Ід№ҷдёӨдқhдәӨжӣҝжӢ?br /> 3 и°ҒжӢҝеҲ°жңҖеҗҺдёҖдёӘзі–жһңжҲ–жңҖеҗҺеҮ дёӘзі–жһңз®—иө?
иҜ·й—®и°Ғжңүеҝ…иғңжҠҠжҸЎ?жҖҺж ·е®һзҺ°?
еҸ‘дҝЎдә? meeme (ҫcійёЈ), дҝЎеҢә: Algorithm
ж ? йў? Re: жӢҝзі–жһңй—®йў?br /> еҸ‘дҝЎз«? ж°ҙжңЁҪC‘ЦҢә (Mon Oct 15 19:26:32 2007), з«ҷеҶ…
иҪ¬жҲҗдәҢиҝӣеҲ?br />
1 =0001
2 =0010
4 =0100
8-1 =0111 +
-----------
0222
ҳqҷж ·жҜҸдёӘдҪҚдёҠйғҪжңүдёӨдёӘ1гҖ?br /> жҜ”еҰӮдёӘдҪҚдёҠпјҢ1е’?еңЁдёӘдҪҚдёҠйғҪжңүдёҖдё?
еҜТҺ–№дёҚеҸҜиғҪеҗҢж—¶жҠҠҳqҷдёӨдё?жӢҝиө°гҖӮжүҖд»ҘеҜ№ж–ТҺҳҜжӢҝдёҚе®Ңзҡ„гҖ?br /> еҜТҺ–№жӢҝе®Ңд№ӢеҗҺеQҢиҮӘе·ұеҶҚжӢҝиӢҘтqІдёӘи°ғж•ҙжҲҗиҝҷҝUҚзҠ¶жҖҒгҖ?br />
дёӯй—ҙеә”иҜҘжңүдёҚһ®‘иҜҒжҳ?..
Ferrersеӣ‘ЦғҸ
дёҖдёӘд»ҺдёҠиҖҢдёӢзҡ„nеұӮж јеӯҗпјҢmi дёә第iеұӮзҡ„ж јеӯҗж•ҺНјҢеҪ“mi>=mi+1(i=1,2,...,n-1) еQҢеҚідёҠеұӮзҡ„ж јеӯҗж•°дёҚе°‘дәҺдёӢеұӮзҡ„ж јеӯҗж•°ж—¶еQҢз§°д№ӢдШ“Ferrersеӣ‘ЦғҸеQҢеҰӮеӣ?2-6-2)ҪCәгҖ?nbsp;

еӣ?nbsp; (2-6-2)
Ferrersеӣ‘ЦғҸе…дhңүеҰӮдёӢжҖ§иҙЁеQ?nbsp;
1.жҜҸдёҖеұӮиҮіһ®‘жңүдёҖдёӘж јеӯҗгҖ?nbsp;
2.ҪW¬дёҖиЎҢдёҺҪW¬дёҖеҲ—дә’жҚўпјҢҪW¬дәҢиЎҢдәҺҪW¬дәҢеҲ—дә’жҚўпјҢ…еQҢеҚіеӣ?2-6-3)ҫl•иҷҡҫUҝибuж—Ӣиқ{жүҖеҫ—зҡ„еӣҫд»Қ然жҳҜFerrersеӣ‘ЦғҸгҖӮдёӨдёӘFerrers еӣ‘ЦғҸҝUоCШ“дёҖеҜ№е…ұиҪӯзҡ„Ferrersеӣ‘ЦғҸгҖ?nbsp;
еҲ©з”ЁFerrersеӣ‘ЦғҸеҸҜеҫ—е…ідәҺж•ҙж•°жӢҶеҲҶзҡ„еҚҒеҲҶжңүӯ‘Јзҡ„ҫl“жһңгҖ?nbsp;
(a)ж•ҙж•°nжӢҶеҲҶжҲҗkдёӘж•°зҡ„е’Ңзҡ„жӢҶеҲҶж•°еQҢе’Ңж•°nжӢҶеҲҶжҲҗдёӘж•°зҡ„е’Ңзҡ„жӢҶеҲҶж•°зӣёҪ{үгҖ?nbsp;
еӣ ж•ҙж•°nжӢҶеҲҶжҲҗkдёӘж•°зҡ„е’Ңзҡ„жӢҶеҲҶеҸҜз”ЁдёҖkиЎҢзҡ„еӣ‘ЦғҸиЎЁзӨәгҖӮжүҖеҫ—зҡ„Ferrersеӣ‘ЦғҸзҡ„е…ұиҪӯеӣҫеғҸжңҖдёҠйқўдёҖиЎҢжңүkдёӘж јеӯҗгҖӮдҫӢеҰӮпјҡ

еӣ?nbsp; (2-6-3)
(b)ж•ҙж•°nжӢҶеҲҶжҲҗжңҖеӨҡдёҚӯ‘…иҝҮmдёӘж•°зҡ„е’Ңзҡ„жӢҶеҲҶж•°еQҢе’ҢnжӢҶеҲҶжҲҗжңҖеӨ§дёҚӯ‘…иҝҮmзҡ„жӢҶеҲҶж•°зӣёзӯүгҖ? зҗҶз”ұе’?a)зӣёзұ»дј№{Җ?nbsp;
еӣ жӯӨеQҢжӢҶеҲҶжҲҗжңҖеӨҡдёҚӯ‘…иҝҮmдёӘж•°зҡ„е’Ңзҡ„жӢҶеҲҶж•°зҡ„жҜҚеҮҪж•°жҳ?nbsp;
![]()
жӢҶеҲҶжҲҗжңҖеӨҡдёҚӯ‘…иҝҮm-1дёӘж•°зҡ„е’Ңзҡ„жӢҶеҲҶж•°зҡ„жҜҚеҮҪж•°жҳ?nbsp;
![]()
жүҖд»ҘжӯЈеҘҪжӢҶеҲҶжҲҗmдёӘж•°зҡ„е’Ңзҡ„жӢҶеҲҶж•°зҡ„жҜҚеҮҪж•°дё?nbsp;

(c)ж•ҙж•°nжӢҶеҲҶжҲҗдә’дёҚзӣёеҗҢзҡ„иӢҘе№ІеҘҮж•°зҡ„е’Ңзҡ„зҡ„жӢҶеҲҶж•?е’ҢnжӢҶеҲҶжҲҗиҮӘе…ЮpҪӯзҡ„Ferrersеӣ‘ЦғҸзҡ„жӢҶеҲҶж•°зӣёзӯү. и®?nbsp;
![]()
е…¶дёӯn1>n2>...>nk
жһ„йҖ дёҖдёӘFerrersеӣ‘ЦғҸеQҢе…¶ҪW¬дёҖиЎҢпјҢҪW¬дёҖеҲ—йғҪжҳҜn1+1ж ы|јҢеҜ№еә”дә?n1+1еQҢ第дәҢиЎҢеQҢ第дәҢеҲ—еҗ„n2+1ж ы|јҢеҜ№еә”дә?n2+1гҖӮд»ҘжӯӨзұ»жҺЁгҖӮз”ұжӯӨеҫ—еҲ°зҡ„Ferresеӣ‘ЦғҸжҳҜе…ұиҪӯзҡ„гҖӮеҸҚҳqҮжқҘд№ҹдёҖж —чҖ?nbsp;
дҫӢеҰӮ 17=9+5+3 еҜ№еә”дёәFerrersеӣ‘ЦғҸдё?

еӣ?nbsp; (2-6-4)
иҙ№еӢ’ж–ҜпјҲFerrersеQүеӣҫиұ?o:p>
еҒҮе®ҡnжӢҶеҲҶдёәn=n1+n2+n3+……+nkеQҢдё”n1>=n2>=n3>=……>=nk
жҲ‘们һ®Ҷе®ғжҺ’еҲ—жҲҗйҳ¶жўҜеЕһеQҢе·Ұиҫ№зңӢйҪҗпјҢжҲ‘们еҸҜд»Ҙеҫ—еҲ°дёҖдёӘзұ»дјјеҖ’йҳ¶жўҜеӣҫеғҸпјҢҳqҷз§Қеӣ‘ЦғҸжҲ‘们ҝUоC№ӢдёәFerrersеӣ‘ЦғҸеQҢеҰӮеҜ№дәҺ20=10+5+4+1еQҢжҲ‘们жңүеӣ‘ЦғҸеQ?/p>
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
|
|
|
||||||||
еҜ№дәҺFerrersеӣ‘ЦғҸеQҢжҲ‘们еҫҲе®ТҺҳ“зҹҘйҒ“д»ҘдёӢдёӨжқЎжҖ§иҙЁеQ?/p>
еQ?еQ?nbsp; жҜҸеұӮиҮӣ_°‘дёҖдёӘж јеӯ?o:p>
еQ?еQ?nbsp; иЎҢеҲ—дә’жҚўеQҢжүҖеҜ№еә”зҡ„еӣҫеғҸд»ҚдёәFerrersеӣ‘ЦғҸеQҢд»–еә”иҜҘдёшҷҜҘеӣ‘ЦғҸзҡ„е…ұиҪӯеӣҫеғ?o:p>
д»АL„Ҹзҡ„Ferrersеӣ‘ЦғҸеҜ№еә”дёҖдёӘж•ҙж•°зҡ„жӢҶеҲҶеQҢиҖҢеҸҜз”ЁFerrersеӣ‘ЦғҸж–№дҫҝең°иҜҒжҳҺпјҡ
еQ?еQ?nbsp; nжӢҶеҲҶдёәkдёӘж•ҙж•°зҡ„жӢҶеҲҶж•ҺНјҢдёҺnжӢҶеҲҶжҲҗжңҖеӨ§ж•°дёәkзҡ„жӢҶеҲҶж•°зӣёзӯү
еQ?еQ?nbsp; nжӢҶеҲҶдёәжңҖеӨҡдёҚӯ‘…иҝҮkдёӘж•°зҡ„жӢҶеҲҶж•°еQҢдёҺnжӢҶеҲҶжҲҗжңҖеӨ§ж•°дёҚи¶…ҳqҮkзҡ„жӢҶеҲҶж•°зӣёзӯү
еQ?еQ?nbsp; nжӢҶеҲҶдёЮZә’дёҚзӣёеҗҢзҡ„иӢҘе№ІеҘҮж•°зҡ„жӢҶеҲҶж•°еQҢдёҺnжӢҶеҲҶжҲҗеӣҫеғҸиҮӘе…ЮpҪӯзҡ„жӢҶеҲҶзҡ„жӢҶеҲҶж•°зӣёҪ{?o:p>
2. Snзҡ„дёҖдёӘжҠҠi1еҸҳеҲ°i2еQҢi2еҸҳеҲ°i3еQ?#8230;…еQҢik-1еҸҳеҲ°ikеQҢikеҸҳеҲ°i1еQҢиҖҢе…¶дҪҷзҡ„е…ғпјҲеҰӮжһңҳqҳжңүеQүдёҚеҸҳзҡ„ҫ|®жҚўҝUоCШ“kйҳ?span style="color: red; font-weight: bold;">еҫӘзҺҜҫ|®жҚў
еҰ?br>(1 2 3 4 5 6) = (1) = (2) = ... = (6)еQҢз§°дёәжҒ’Ҫ{үзҪ®жҚ?br> 1 2 3 4 5 6
3.еҮ дёӘе®ҡзҗҶеQ?br>1) и®ҫfеQҢgдёЮZёӨдёӘдёҚзӣжҖәӨзҡ„еу@зҺҜзҪ®жҚўпјҢеҲҷfg = gf
2) д»АL„Ҹҫ|®жҚўеқҮеҸҜе”ҜдёҖең°еҲҶи§ЈжҲҗдёҚзӣёдәӨеу@зҺҜзҪ®жҚўзҡ„д№ҳз§Ҝ
ҳqҷдёӘе®ҡзҗҶеҸҜз”ұжһ„йҖ жі•иҜҒеҫ—еQҢиҜҘиҜҒжі•еҗҢж—¶д№ҹз»ҷеҮЮZәҶеҲҶи§Јдёәеу@зҺҜзҪ®жҚўзҡ„д№ҳз§Ҝзҡ„ж–№жі?br>3) д»АL„Ҹҫ|®жҚўеқҮеҸҜеҲҶи§ЈдёәеҜ№жҚўзҡ„д№ҳз§ҜеQҲдёҚе”ҜдёҖеQүпјҢдҫӢеҰӮ
(12)(345) = (12)(35)(34) = (12)(14)(41)(35)(34)
4. ҫ|®жҚўзҡ„еҘҮеҒ¶жҖ?br>1) и®ҫf ∈SnеQҢ规е®ҡfзҡ„з¬ҰеҸ·дШ“
Sgn f = ∏[ f(i) - f(j) ] / (i - j)
иІҢдјјһ®ұжҳҜйҖҶеәҸеҜТҺ•°зҡ„еҘҮеҒ¶жҖ§пјҢеҘҮдШ“-1еQҢеҒ¶дё?
2) Sgn(fg) = (Sgn f)(Sgn g)
3) n > 1ж—УһјҢSnдёӯеҘҮҫ|®жҚўдёҺеҒ¶ҫ|®жҚўзҡ„дёӘж•°зӣёҪ{үпјҢеқҮдШ“n! / 2
еҸҜйҖҡиҝҮеҲҶзҰ»дёҖҫl„еҜ№жҚўз§ҜиҜҒеҫ—
ҪW¬дәҢеQҢиҜҒжҳҺSжҳҜеҪ’ҫUійӣҶ
2. и®ҫAдёЮZёҖдёӘйӣҶеҗҲпјҢеҰӮжһңAдёӯд“QдҪ•е…ғзҙ зҡ„е…ғзҙ д№ҹжҳҜAзҡ„е…ғзҙ пјҢеҲҷз§°Aдё?strong style="COLOR: red">дј йҖ’йӣҶгҖӮжҜҸдёӘиҮӘ然数йғҪжҳҜдј йҖ’йӣҶгҖ?br>д»ҘдёӢе‘ҪйўҳҪ{үдӯhеQ?br>(1) AжҳҜдј йҖ’йӣҶ
(2) ∪A еҢ…еҗ«дә?A
(3) еҜ№дәҺд»АL„Ҹзҡ„y∈AеQҢyеҢ…еҗ«дәҺA
(4) AеҢ…еҗ«дәҺP(A)
(5) P(A)дёЮZј йҖ’йӣҶ
3. и®ҫAдёЮZёҖдёӘйӣҶеҗҲпјҢҝUоC»ҺA*AеҲ°Aзҡ„еҮҪж•оCШ“AдёҠзҡ„дәҢе…ғҳqҗз®—гҖ?br>еҸ?: N*N -> NеQҢдё”еҜ№дәҺд»АL„Ҹзҡ„m, n ∈NеQ?(<m, n>) = Am(n), и®оCҪңm + nеQҢз§°+дёәNдёҠзҡ„еҠ жі•ҳqҗз®—
еҸ?#183;: N*N -> NеQҢдё”еҜ№дәҺд»АL„Ҹзҡ„m, n ∈NеQ?#183;(<m, n>) = Mm(n)еQҢи®°дҪңm·nеQҢз§°·дёәNдёҠзҡ„д№ҳжі•ҳqҗз®—гҖ?br>
PeanoҫpИқ»ҹжҳҜж»Ўӯ‘ід»ҘдёӢе…¬и®„Ўҡ„жңүеәҸдёүе…ғҫl?lt;M, F, e>еQҢе…¶дёӯMдёЮZёҖдёӘйӣҶеҗҲпјҢFдёәMеҲ°Mзҡ„еҮҪж•ҺНјҢeдёәйҰ–е…ғзҙ гҖ?жқЎе…¬и®ҫдШ“еQ?/p>
(1) e ∈M
(2) MеңЁFдёӢжҳҜһ®Ғй—ӯзҡ?br>(3) e еK?ranF еQҲжҡӮж—¶еҸӘжү‘ЦҲ°ҳqҷдёӘҪWҰеҸ·иЎЁзӨә“дёҚеұһдә?#8221; еӣ§пјү
(4) FжҳҜеҚ•һ®„зҡ„
(5) еҰӮжһңMзҡ„еӯҗйӣҶAж»Ўиғц (eеұһдәҺA) дё?(AеңЁFдёӢжҳҜһ®Ғй—ӯзҡ?еQҢеҲҷA=M
(5)ҝUоCШ“жһҒе°ҸжҖ§е…¬и®?br>
2. и®ҫAдёЮZёҖдёӘйӣҶеҗҲпјҢҝU?A∪{A} дёәAзҡ?strong style="COLOR: red">еҗҺз‘феQҢи®°дҪңA+, тq¶з§°жұӮйӣҶеҗҲзҡ„еҗҺз‘фдё?span style="COLOR: red">еҗҺз‘фҳqҗз®—гҖ?br>
3. и®ҫAдёЮZёҖдёӘйӣҶеҗҲпјҢиӢҘAж»ЎиғцеQ?br>(1) Ø ∈AеQ?br>(2) иӢҘеҜ№дәҺдёҖеҲ?a ∈AеQҢеҲҷ a+ ∈AеQ?br>еҲҷз§°Aжҳ?strong style="COLOR: red">еҪ’зәійӣ?/strong>гҖ?br>
4. д»ҺеҪ’ҫUійӣҶзҡ„е®ҡд№үеҸҜд»ҘзңӢеҮәпјҢØеQ?#216;+, Ø++,... жҳҜжүҖжңүеҪ’ҫUійӣҶзҡ„е…ғзҙ пјҢдәҺжҳҜеҸҜд»Ҙһ®Ҷе®ғ们е®ҡд№үжҲҗиҮӘ然ж•?/strong>гҖ?br>иҮӘ然数жҳҜеұһдәҺжҜҸдёӘеҪ’зәійӣҶзҡ„йӣҶеҗҲеQҢе°ҶØеQ?#216;+, Ø++,...еҲҶеҲ«и®оCШ“0, 1, 2, ...
и®ҫD={v | vжҳҜеҪ’ҫUійӣҶ|еQҢз§°∩Dдёәе…ЁдҪ“иҮӘ然数йӣҶеҗҲеQҢи®°дёәN.
и®ҫNдёшҷҮӘ然数йӣҶеҗҲеQ?#963;: N -> NеQҢдё”σ(n) = n+, еҲ?lt;N, σ, Ø>жҳҜPeanoҫpИқ»ҹгҖ?br>ҳqҷдёӘPeanoҫpИқ»ҹзҡ„第(5)жқЎе…¬и®ҫжҸҗеҮЮZәҶиҜҒжҳҺиҮӘ然数жҖ§иҙЁзҡ„дёҖҝUҚж–№жі•пјҢеҚ?span style="COLOR: red">ж•°еӯҰеҪ’зәіжі?/strong>еQҢз§°жӯӨе…¬и®ҫдШ“ж•°еӯҰеҪ’зәіжі•еҺҹзҗ?/strong>гҖ?/p>
еҜ№з§° symmetric
дј йҖ?transitive
(2) е…¶дёӯеQҢи®ҫRеұһдәҺA*AеQҲAдёәйқһҪIәйӣҶеҗҲпјүеQҢеҲҷr(R) = RдёҺAдёҠжҒ’Ҫ{үе…іҫpИқҡ„тqУһјҢs(R) = RдёҺRзҡ„йҖҶзҡ„тqУһјҢ
t(R) = R тq?R^2 тq?R^3 тq?..тq?R^lгҖ?br>(3) rs(R) = sr(R)
rt(R) = tr(R)
st(R) еұһдәҺ ts(R)
2. Ҫ{үдӯhе…ізі»е’ҢеҲ’еҲ?br>(1) и®ҫRеұһдәҺA*AеQҢиӢҘRжҳҜиҮӘеҸҚзҡ„гҖҒеҜ№ҝU°зҡ„е’Ңдј йҖ’зҡ„еQҢеҲҷҝU°RдёәAдёҠзҡ„Ҫ{үдӯhе…ізі»гҖ?br>(2) д»Ө[x]Rдёәxзҡ„е…ідәҺRзҡ„зӯүд»пLұ»еQҢеңЁдёҚеј•иөдhШңд№ұж—¶еҸҜз®Җи®оCШ“[x]гҖ?br>(3) д»Ҙе…ідәҺRзҡ„е…ЁдҪ“дёҚеҗҢзҡ„Ҫ{үдӯhҫcЦMШ“е…ғзҙ зҡ„йӣҶеҗҲз§°дёәAе…ідәҺRзҡ„е•ҶйӣҶпјҢи®оCҪңA/RгҖ?br>(4) и®ҫAдёәйқһҪIәйӣҶеҗҲпјҢиӢҘеӯҳеңЁAзҡ„дёҖдёӘеӯҗйӣҶж—ҸSж»Ўиғц
a. SдёӯдёҚеҢ…еҗ«ҪIәйӣҶе…ғзҙ
b. еҜ№дәҺдёҖеҲҮx,yеұһдәҺSеQҢдё”x,yдёҚзӣёҪ{үпјҢеҲҷxдёҺyдёҚзӣёдәӨзҡ„(disjoint)
c. SдёӯжүҖжңүйӣҶеҗҲзҡ„тq¶дШ“A
еҲҷз§°SдёәAзҡ„дёҖдёӘеҲ’еҲҶпјҢSдёӯе…ғзҙ з§°дёәеҲ’еҲҶеқ—гҖ?br>(5) йқһз©әйӣҶеҗҲAдёҠзҡ„Ҫ{үдӯhе…ізі»дёҺAзҡ„еҲ’еҲҶжҳҜдёҖдёҖеҜ№еә”зҡ„гҖ?br>(6) ҪW¬дәҢҫc»Stirlingж•ҺНјҢиЎЁзӨәһ®ҶnдёӘдёҚеҗҢзҡ„зҗғж”ҫе…ҘrдёӘзӣёеҗҢзҡ„зӣ’еӯҗдёӯзҡ„ж–ТҺЎҲж•ҺНјҢеҸҜд»Ҙз”ЧғёӢеҲ—йҖ’еҪ’ејҸи®ЎҪҺ—пјҡ
f(n, r) = r * f(n - 1, r) + f(n - 1, r - 1)
еҫҲе®№жҳ“зҗҶи§Јзҡ„дёҖдёӘйҖ’еҪ’ејҸпјҢе…¶дёӯеҲқе§ӢзҠ¶жҖҒдШ“
f(n, 0) = 0, f(n, 1) = 1, f(n, 2) = 2^(n-1) - 1, f(n, n - 1) = C(n, 2), f(n, n) = 1
(7) AдёҠзӯүд»·е…іҫpИқҡ„ж•°йҮҸеҸҜд»ҘйҖҡиҝҮStiringж•°жұӮеҮәпјҢд»ҘA={a,b,c,d}дёЮZҫӢ
f(4,1) + f(4,2) + f(4,3) + f(4,4) = 15
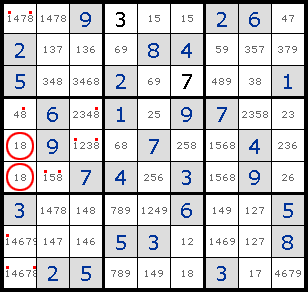
1. Intersection жЁӘж–ӯеQҢжёёжҲҸдёҖејҖе§Ӣе°ұдҪҝз”Ёзҡ„еёёи§ҒжҠҖе·§гҖ?/p>
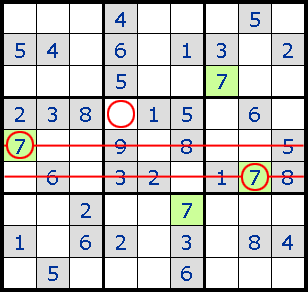
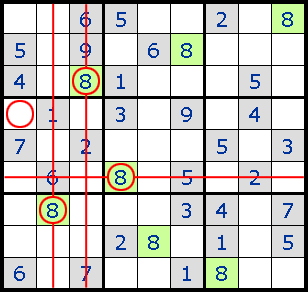
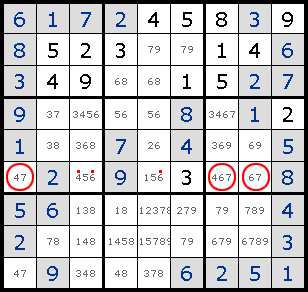
2. Forced Moves жҺ’йҷӨжүҖжңүе…¶д»–еҸҜиғҪжҖ§еҗҺе”ҜдёҖзҡ„зӯ”жЎ?br>
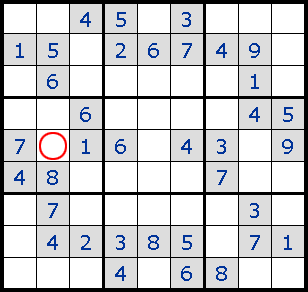
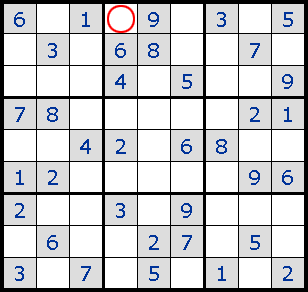
3. Pinned Squares
Intersection зҡ„еҠ ејәзүҲеQҢж №жҚ®жӣҙеӨҡзҡ„жғ…еҶөјӢ®е®ҡжҹҗдёҖдёӘж•°еӯ—еңЁиҜҘеҢәеҹҹзҡ„е”ҜдёҖеҸҜиғҪдҪҚзҪ®гҖ?br>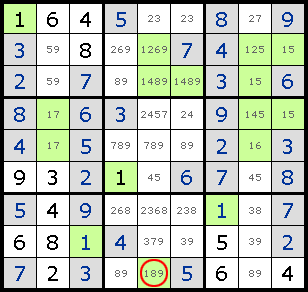
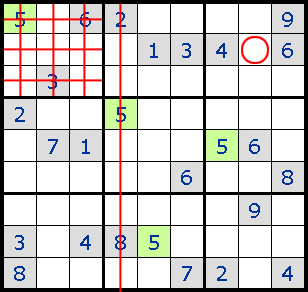
4. Locked Sets
еҰӮеӣҫдёҖR5C1е’ҢR6C1еҸӘиғҪеЎ?жҲ?еQҢз”ұжӯӨеҸҜжҺ’йҷӨдёҺ他们жңүе…ізҡ„еҹҹдёӯзҡ„е…¶д»–ж јеЎ?е’?зҡ„еҸҜиғҪжҖ§пјҢд»ҺиҖҢR6C2еҸӘиғҪеЎ?гҖ?/p>