本文github地址

本文以Java TreeMap為例，從源代碼層面，結(jié)合詳細(xì)的圖解，剝繭抽絲地講解紅黑樹(shù)（Red-Black tree）的插入，刪除以及由此產(chǎn)生的調(diào)整過(guò)程。

總體介紹

Java TreeMap實(shí)現(xiàn)了SortedMap接口，也就是說(shuō)會(huì)按照key的大小順序?qū)?em>Map中的元素進(jìn)行排序，key大小的評(píng)判可以通過(guò)其本身的自然順序（natural ordering），也可以通過(guò)構(gòu)造時(shí)傳入的比較器（Comparator）。

TreeMap底層通過(guò)紅黑樹(shù)（Red-Black tree）實(shí)現(xiàn)，也就意味著containsKey(), get(), put(), remove()都有著log(n)的時(shí)間復(fù)雜度。其具體算法實(shí)現(xiàn)參照了《算法導(dǎo)論》。

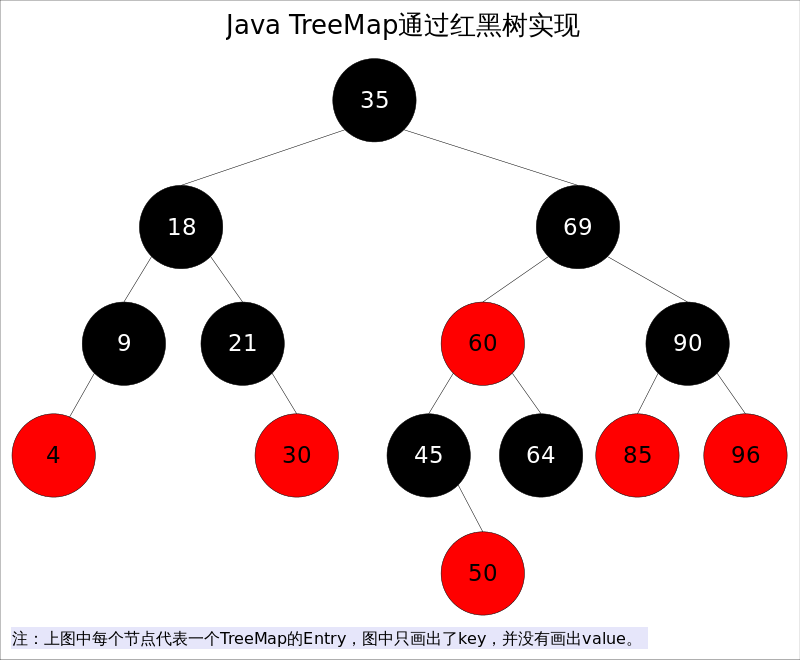
出于性能原因，TreeMap是非同步的（not synchronized），如果需要在多線(xiàn)程環(huán)境使用，需要程序員手動(dòng)同步；或者通過(guò)如下方式將TreeMap包裝成（wrapped）同步的：

SortedMap m = Collections.synchronizedSortedMap(new TreeMap(...));

紅黑樹(shù)是一種近似平衡的二叉查找樹(shù)，它能夠確保任何一個(gè)節(jié)點(diǎn)的左右子樹(shù)的高度差不會(huì)超過(guò)二者中較低那個(gè)的一陪。具體來(lái)說(shuō)，紅黑樹(shù)是滿(mǎn)足如下條件的二叉查找樹(shù)（binary search tree）：

1. 每個(gè)節(jié)點(diǎn)要么是紅色，要么是黑色。
2. 根節(jié)點(diǎn)必須是黑色
3. 紅色節(jié)點(diǎn)不能連續(xù)（也即是，紅色節(jié)點(diǎn)的孩子和父親都不能是紅色）。
4. 對(duì)于每個(gè)節(jié)點(diǎn)，從該點(diǎn)至null（樹(shù)尾端）的任何路徑，都含有相同個(gè)數(shù)的黑色節(jié)點(diǎn)。

在樹(shù)的結(jié)構(gòu)發(fā)生改變時(shí)（插入或者刪除操作），往往會(huì)破壞上述條件3或條件4，需要通過(guò)調(diào)整使得查找樹(shù)重新滿(mǎn)足紅黑樹(shù)的條件。

預(yù)備知識(shí)

前文說(shuō)到當(dāng)查找樹(shù)的結(jié)構(gòu)發(fā)生改變時(shí)，紅黑樹(shù)的條件可能被破壞，需要通過(guò)調(diào)整使得查找樹(shù)重新滿(mǎn)足紅黑樹(shù)的條件。調(diào)整可以分為兩類(lèi)：一類(lèi)是顏色調(diào)整，即改變某個(gè)節(jié)點(diǎn)的顏色；另一類(lèi)是結(jié)構(gòu)調(diào)整，集改變檢索樹(shù)的結(jié)構(gòu)關(guān)系。結(jié)構(gòu)調(diào)整過(guò)程包含兩個(gè)基本操作：左旋（Rotate Left），右旋（RotateRight）。

左旋

左旋的過(guò)程是將x的右子樹(shù)繞x逆時(shí)針旋轉(zhuǎn)，使得x的右子樹(shù)成為x的父親，同時(shí)修改相關(guān)節(jié)點(diǎn)的引用。旋轉(zhuǎn)之后，二叉查找樹(shù)的屬性仍然滿(mǎn)足。

TreeMap中左旋代碼如下：

右旋

右旋的過(guò)程是將x的左子樹(shù)繞x順時(shí)針旋轉(zhuǎn)，使得x的左子樹(shù)成為x的父親，同時(shí)修改相關(guān)節(jié)點(diǎn)的引用。旋轉(zhuǎn)之后，二叉查找樹(shù)的屬性仍然滿(mǎn)足。

TreeMap中右旋代碼如下：

方法剖析

get()

get(Object key)方法根據(jù)指定的key值返回對(duì)應(yīng)的value，該方法調(diào)用了getEntry(Object key)得到相應(yīng)的entry，然后返回entry.value。因此getEntry()是算法的核心。算法思想是根據(jù)key的自然順序（或者比較器順序）對(duì)二叉查找樹(shù)進(jìn)行查找，直到找到滿(mǎn)足k.compareTo(p.key) == 0的entry。

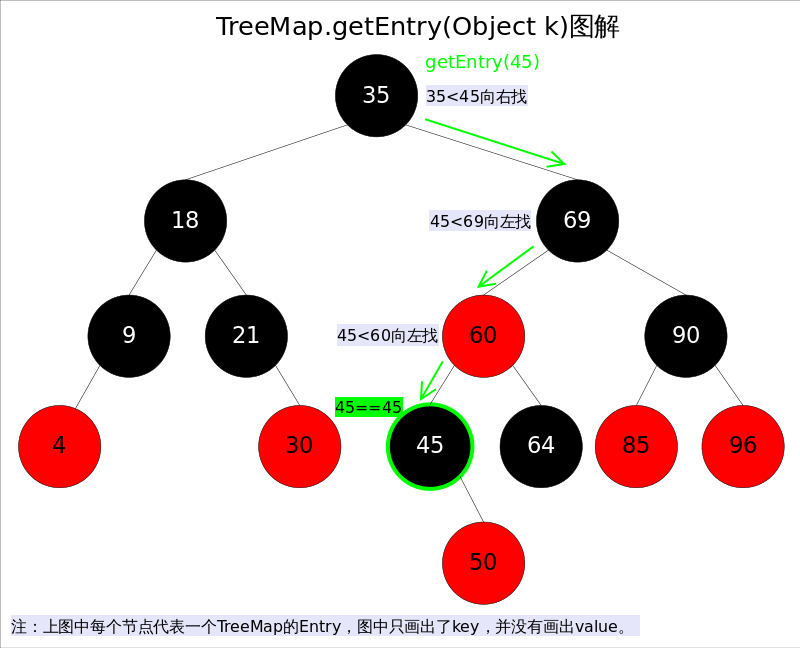
具體代碼如下：

//getEntry()方法
final Entry<K,V> getEntry(Object key) {
    
    if (key == null)//不允許key值為null
        throw new NullPointerException();
    Comparable<? super K> k = (Comparable<? super K>) key;//使用元素的自然順序
    Entry<K,V> p = root;
    while (p != null) {
        int cmp = k.compareTo(p.key);
        if (cmp < 0)//向左找
            p = p.left;
        else if (cmp > 0)//向右找
            p = p.right;
        else
            return p;
    }
    return null;
}

put()

put(K key, V value)方法是將指定的key, value對(duì)添加到map里。該方法首先會(huì)對(duì)map做一次查找，看是否包含該元組，如果已經(jīng)包含則直接返回，查找過(guò)程類(lèi)似于getEntry()方法；如果沒(méi)有找到則會(huì)在紅黑樹(shù)中插入新的entry，如果插入之后破壞了紅黑樹(shù)的約束，還需要進(jìn)行調(diào)整（旋轉(zhuǎn)，改變某些節(jié)點(diǎn)的顏色）。

public V put(K key, V value) {
    
    int cmp;
    Entry<K,V> parent;
    if (key == null)
        throw new NullPointerException();
    Comparable<? super K> k = (Comparable<? super K>) key;//使用元素的自然順序
    do {
        parent = t;
        cmp = k.compareTo(t.key);
        if (cmp < 0) t = t.left;//向左找
        else if (cmp > 0) t = t.right;//向右找
        else return t.setValue(value);
    } while (t != null);
    Entry<K,V> e = new Entry<>(key, value, parent);//創(chuàng)建并插入新的entry
    if (cmp < 0) parent.left = e;
    else parent.right = e;
    fixAfterInsertion(e);//調(diào)整
    size++;
    return null;
}

上述代碼的插入部分并不難理解：首先在紅黑樹(shù)上找到合適的位置，然后創(chuàng)建新的entry并插入（當(dāng)然，新插入的節(jié)點(diǎn)一定是樹(shù)的葉子）。難點(diǎn)是調(diào)整函數(shù)fixAfterInsertion()，前面已經(jīng)說(shuō)過(guò)，調(diào)整往往需要1.改變某些節(jié)點(diǎn)的顏色，2.對(duì)某些節(jié)點(diǎn)進(jìn)行旋轉(zhuǎn)。

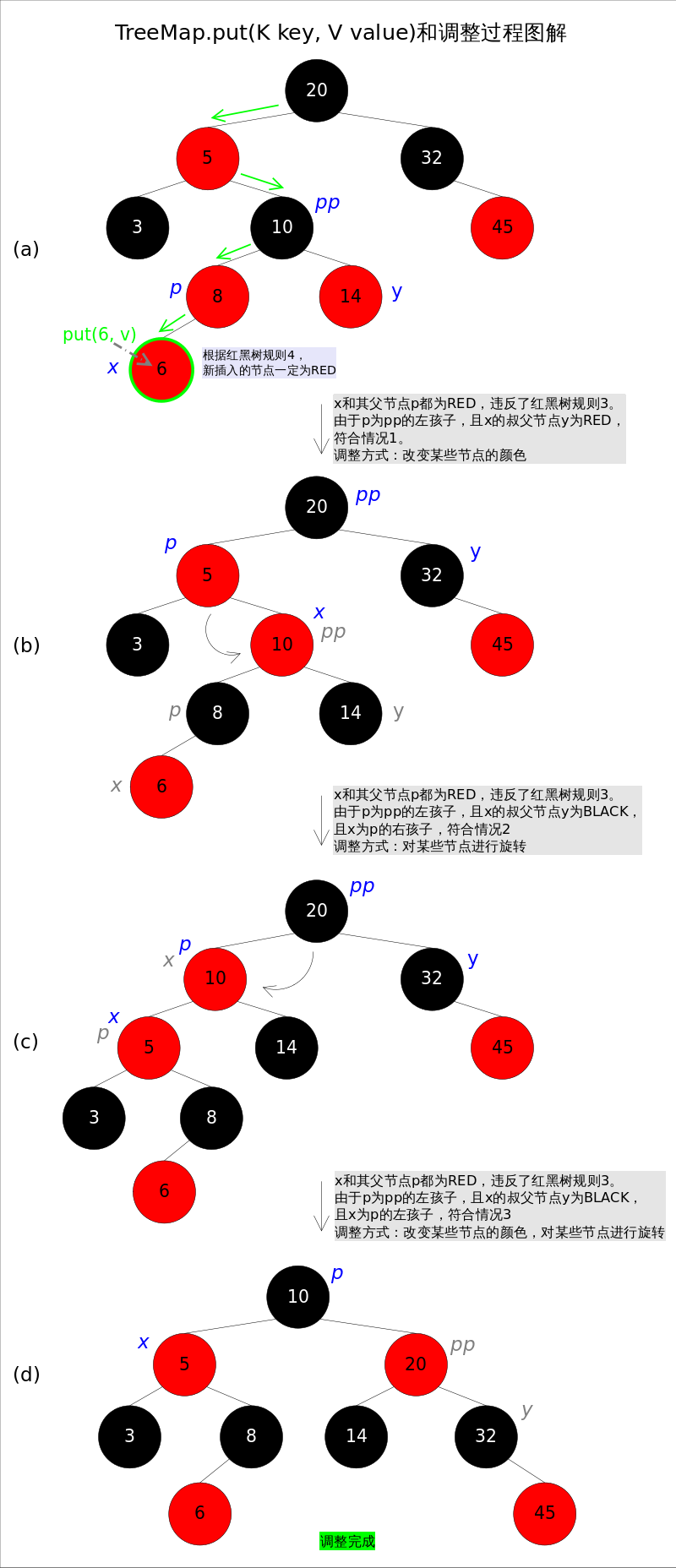
調(diào)整函數(shù)fixAfterInsertion()的具體代碼如下，其中用到了上文中提到的rotateLeft()和rotateRight()函數(shù)。通過(guò)代碼我們能夠看到，情況2其實(shí)是落在情況3內(nèi)的。情況4～情況6跟前三種情況是對(duì)稱(chēng)的，因此圖解中并沒(méi)有畫(huà)出后三種情況，讀者可以參考代碼自行理解。

remove()

remove(Object key)的作用是刪除key值對(duì)應(yīng)的entry，該方法首先通過(guò)上文中提到的getEntry(Object key)方法找到key值對(duì)應(yīng)的entry，然后調(diào)用deleteEntry(Entry<K,V> entry)刪除對(duì)應(yīng)的entry。由于刪除操作會(huì)改變紅黑樹(shù)的結(jié)構(gòu)，有可能破壞紅黑樹(shù)的約束，因此有可能要進(jìn)行調(diào)整。

有關(guān)remove()的具體講解將放到下一篇博文當(dāng)中，敬請(qǐng)期待！