樹的特點:
1. 每個結點有零個或多個子結點
2. 每一個子結點只有一個父結點
3. 沒有前驅的結點為根結點
4. 除了根結點外,每個子結點可以分為m個不相交的子樹
樹相關的術語:
節點的度:一個節點含有的子樹的個數稱為該節點的度
葉節點或終端節點:度為零的節點稱為葉節點
非終端節點或分支節點:度不為零的節點
雙親節點或父節點:若一個結點含有子節點,則這個節點稱為其子節點的父節點
孩子節點或子節點:一個節點含有的子樹的根節點稱為該節點的子節點
兄弟節點:具有相同父節點的節點互稱為兄弟節點
樹的度:一棵樹中,最大的節點的度稱為樹的度
節點的層次:從根開始定義起,根為第1層,根的子節點為第2層,以此類推
樹的高度或深度:樹中節點的最大層次
堂兄弟節點:雙親在同一層的節點互為堂兄弟
節點的祖先:從根到該節點所經分支上的所有節點
子孫:以某節點為根的子樹中任一節點都稱為該節點的子孫
森林:由m(m>=0)棵互不相交的樹的集合稱為森林
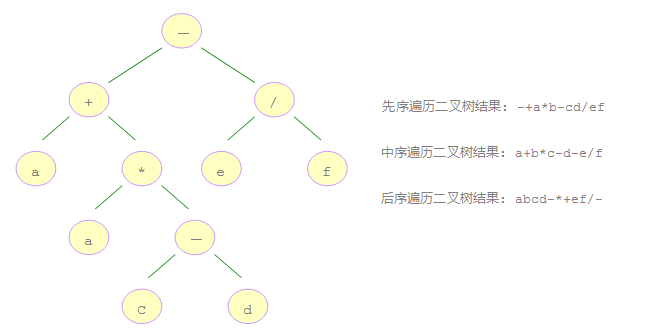
二叉樹 是每個節點最多有兩個子樹的樹結構,如上圖。
/**
* <!--
* File : binarytree.h
* Author : fancy
* Email : fancydeepin@yeah.net
* Date : 2013-02-03
* --!>
*/
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#define Element char
#define format "%c"
typedef struct Node {
Element data;
struct Node *lchild;
struct Node *rchild;
} *Tree;
int index = 0; //全局索引變量
//二叉樹構造器,按先序遍歷順序構造二叉樹
//無左子樹或右子樹用'#'表示
void treeNodeConstructor(Tree &root, Element data[]){
Element e = data[index++];
if(e == '#'){
root = NULL;
}else{
root = (Node *)malloc(sizeof(Node));
root->data = e;
treeNodeConstructor(root->lchild, data); //遞歸構建左子樹
treeNodeConstructor(root->rchild, data); //遞歸構建右子樹
}
}
//先序遍歷二叉樹
void preorderTraversal(Tree root){
if(root){
printf(format, root->data);
preorderTraversal(root->lchild);
preorderTraversal(root->rchild);
}
}
//中序遍歷二叉樹
void inorderTraversal(Tree root){
if(root){
inorderTraversal(root->lchild);
printf(format, root->data);
inorderTraversal(root->rchild);
}
}
//后序遍歷二叉樹
void postorderTraversal(Tree root){
if(root){
postorderTraversal(root->lchild);
postorderTraversal(root->rchild);
printf(format, root->data);
}
}
/**
* <!--
* File : BinaryTree.cpp
* Author : fancy
* Email : fancydeepin@yeah.net
* Date : 2013-02-03
* --!>
*/
#include "binarytree.h"
int main() {
//上圖所示的二叉樹先序遍歷序列,其中用'#'表示結點無左子樹或無右子樹
Element data[23] = {'-', '+', 'a', '#', '#', '*', 'b', '#', '#', '-', 'c',
'#', '#', 'd', '#', '#', '/', 'e', '#', '#', 'f', '#', '#'};
Tree tree;
treeNodeConstructor(tree, data);
printf("------------------------------------\n");
printf("\nCreate binary tree successfully!\n");
printf("\n------------------------------------");
printf("\n\n先序遍歷二叉樹結果: ");
preorderTraversal(tree);
printf("\n\n中序遍歷二叉樹結果: ");
inorderTraversal(tree);
printf("\n\n后序遍歷二叉樹結果: ");
postorderTraversal(tree);
system("pause");
return 0;
}
posted on 2013-02-03 11:11
fancydeepin 閱讀(1893)
評論(0) 編輯 收藏