圖
-
實驗?zāi)康?/span>
熟悉圖的兩種常用的存儲結(jié)構(gòu)，以及在這兩種存儲結(jié)構(gòu)上的兩種遍歷圖的方法，即深
度優(yōu)先遍歷和廣度優(yōu)先遍歷。進一步掌握遞歸算法的設(shè)計方法。
關(guān)于各種典型著名的復(fù)雜算法，在上機實習(xí)方面不做基本要求。更適合于安排大型課
程設(shè)計。
二.需求分析
本程序演示用C++編寫,完成有向圖的創(chuàng)建,用Prim算法實現(xiàn)最小生成樹,實現(xiàn)邊的插入和刪除.
輸入值的范圍:創(chuàng)建圖時要求輸入的結(jié)點個數(shù)不大于MaxVertices的值.在插入邊時要求原圖不存在起點和終點之間邊,并且插入的邊不是矩陣對角線上的邊.輸入的數(shù)據(jù)類型為整形.
輸出形式:以鄰接矩陣的形式輸出圖的數(shù)據(jù)項.如果操作非法則給出錯誤信息.
測試數(shù)據(jù)
A創(chuàng)建5個頂點4條邊的圖:輸入頂點分別為1,2,3,4,5;1和2之間,2和3之間,3和4 之間,4和5之間的權(quán)值分別為10,20,30,40.得到圖:
輸出頂點的信息（整型）：
1 2 3 4 5
輸出鄰接矩陣 ：
1: 0 10 1000 1000 1000
2: 1000 0 20 1000 1000
3: 1000 1000 0 30 1000
4: 1000 1000 1000 0 40
5: 1000 1000 1000 1000 0
B頂點4和3之間插入一條權(quán)值為50邊得
輸出頂點的信息（整型）：
1 2 3 4 5
輸出鄰接矩陣 ：
1: 0 10 1000 1000 1000
2: 1000 0 20 1000 1000
3: 1000 1000 0 30 1000
4: 1000 1000 50 0 40
5: 1000 1000 1000 1000 0
C刪除頂點4和3之間的邊得
輸出頂點的信息（整型）：
1 2 3 4 5
輸出鄰接矩陣 ：
1: 0 10 1000 1000 1000
2: 1000 0 20 1000 1000
3: 1000 1000 0 30 1000
4: 1000 1000 1000 0 40
5: 1000 1000 1000 1000 0
三.設(shè)計概要
(1)為了實現(xiàn)上述程序的功能,需要定義圖的抽象數(shù)據(jù)類型:
ADT Graph is{
數(shù)據(jù)對象：D={ai|ai∈IntegerSet,i=0,1,2,…,n,n≥0}
基本操作:
CreatG()
操作結(jié)果:創(chuàng)建有向圖
InsertE()
初始條件:有向圖已經(jīng)存在
操作結(jié)果:插入一條邊
DeleteE ()
初始條件: 有向圖已經(jīng)存在
操作結(jié)果:刪除一條邊
}END ADT BiTree
(2) 本程序包含一個類和一個結(jié)構(gòu)體類型
A無向圖類AdjMWGraph有7個函數(shù)
1主函數(shù) main()
2.構(gòu)造函數(shù) AdjMWGraph()
3. 創(chuàng)建圖函數(shù) CreatG(int n,int e)
4. 插入邊函數(shù) InsertE()
5. 刪除邊函數(shù) DeleteE()
6. 求最小生成樹Prim算法函數(shù) Prim()
B結(jié)構(gòu)體類型MinSpanTree
(3)本程序的兩個文件
1.頭文件 Graph.h
2.源文件 Graph.cpp
(4)函數(shù)之間的關(guān)系
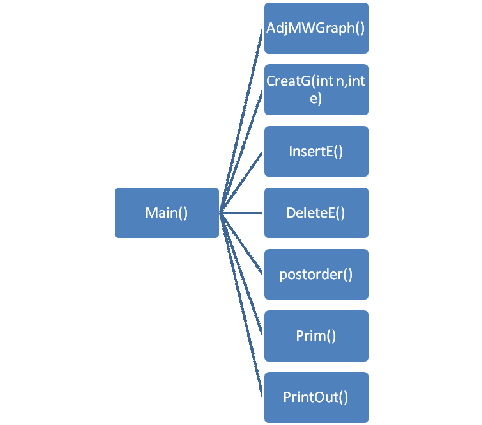
四.詳細設(shè)計
1
//Graph.h
2#include "iostream"
3#include <iomanip>
4#include <stdlib.h>
5using namespace std;
6const int MaxVertices=10;
7const int MaxWeight=1000;
8struct MinSpanTree //帶權(quán)邊的三個參數(shù)
9
{
10
int begin,end; //邊的起點與終點
11 int length; //邊的權(quán)值
12
};
13
14class AdjMWGraph
15{
16private:
17 int Vertices[20]; //頂點信息的數(shù)組
18 int Edge[MaxVertices][MaxVertices]; //邊的權(quán)信息的矩陣
19 int numE; //當(dāng)前的邊數(shù)
20 int numV; //當(dāng)前的頂點數(shù)
21public:
22 AdjMWGraph(); //構(gòu)造函數(shù)
23 void CreatG(int n,int e); //創(chuàng)建圖函數(shù)
24 void PrintOut(); //打印圖中數(shù)據(jù)項函數(shù)
25 void Prim() ; //求最小生成樹方法(Prim算法)
26 void InsertE(); //插入邊函數(shù)
27 void DeleteE(); //刪除邊函數(shù)
28};
29//Graph.cpp
30#include "Graph.h"
31
32//初始化矩陣
33AdjMWGraph::AdjMWGraph() //構(gòu)造函數(shù)
34{
35 //初始化矩陣為
36 for ( int i = 0; i < MaxVertices; i++ ) //行
37 for ( int j = 0; j < MaxVertices; j++ ) //列
38
{
39 if( i==j )
40 Edge[i][j] = 0; //對角線置零
41 else
42 Edge[i][j] = MaxWeight; //無邊時權(quán)值置這無窮大
43
}
44 numE = 0; //當(dāng)前邊個數(shù)初始為
45 numV = 0; //當(dāng)前的頂點個數(shù)為
46}
47
48//創(chuàng)建圖
49void AdjMWGraph::CreatG(int n,int e)
50{
51 int vi,vj,w;
52 numE = e;
53 numV = n;
54 cout<<"\n 輸入頂點的信息（整型）：" ;
55
56 //頂點賦值
57 for (int i = 0; i < numV; i++ )
58 {
59 cout<<"\n "<<i+1<<": ";
60 cin >> Vertices[i];
61
62 }
63
64 //邊賦權(quán)值
65 for ( int i = 0; i < numE;)
66 {
67 cout<<"\n 輸入邊的信息（vi,vj,W）：";
68 cin >> vi >> vj >> w;
69
70//判斷起點和終點是否存在,是否是對角線上的點并且邊是否存在
71 if ((vi != vj )
72 && (vi>0 && vi<=numV)
73 && (vj>0 && vj<=numV)
74 && (Edge[vi-1][vj-1] == MaxWeight))
75 {
76 Edge[vi-1][vj-1] = w; //更改對應(yīng)的行和列的權(quán)值
77 i++;
78 }
79 else
80 {
81 cout << "\t插入位置錯誤或邊已經(jīng)存在!\n\t請正確輸入." <<endl;
82 }
83 }
84 }
85
86//打印圖中數(shù)據(jù)項
87void AdjMWGraph::PrintOut()
88{
89 cout << "\n 輸出頂點的信息（整型）：\n";
90 for ( int i = 0; i < numV; i++ )
91 cout << "\t" << Vertices[i] ;
92 cout << "\n 輸出鄰接矩陣：" <<endl;
93 for ( int i = 0; i < numV; i++ )
94 {
95 cout << "\n "<< i+1 <<": ";
96 for ( int j = 0; j < numV ; j++ )
97 cout << "\t" << Edge[i][j] ;
98 cout << endl;
99 }
100 }
101
102//Prim普里姆算法求最小生成樹
103void AdjMWGraph::Prim ()
104{
105 int n = numV,m,v; //頂點總數(shù)
106 MinSpanTree e, mintree[MaxVertices]; // mintree 生成樹數(shù)組
107
108 for (int j = 1; j < n; j++) //初始化tree[n-1]
109 {
110 mintree[j-1].begin = 1; //頂點并入U
111 mintree[j-1].end = j+1;
112 mintree[j-1].length = Edge[0][j]; // G.Edge[][]是連通網(wǎng)的帶權(quán)鄰接矩陣
113 }
114
115 for (int k = 0; k < n-1; k++) // 求第k+1條邊
116 {
117 int min = MaxWeight;
118
119 for (int j = k; j < n-1; j++)
120 if (mintree[j].length < min ) //求鄰接的最小的邊
121 {
122 min = mintree[j].length;
123 m = j;
124 } //for j
125
126 //交換方法置下個鄰接點為終點
127 e = mintree[m];
128 mintree[m] = mintree[k];
129 mintree[k] = e;
130 v = mintree[k].end; //V∈U
131
132 for (int j = k+1; j < n-1; j++) //在新的頂點v并入U之后更新tree[n-1]
133 {
134 int d = Edge[v-1][mintree[j].end-1];
135 if (d < mintree[j].length) //循環(huán)找到與當(dāng)前點相鄰的最小權(quán)值的邊
136 {
137 mintree[j].length = d;
138 mintree[j].begin = v; //置當(dāng)前點為起點
139 }
140 }// for k
141 }
142 for (int j = 0;j < n-1; j++)
143 cout<<"\n"<<"起點："<< mintree[j].begin <<" 終點："<<
144 mintree[j].end<<" 權(quán)值："<<mintree[j].length;
145 cout << endl;
146}
147
148//插入一條的算法
149void AdjMWGraph::InsertE()
150{
151 int i,j,w;
152 cout << "\n 請輸入插入邊的起點,終點和權(quán)值(vi,vj,W):";
153 cin >> i >> j >> w;
154 //判斷起點各終點是否存在并且不是對角線上的點
155 if ( ( i != j ) && (i>0 && i<=numV) && (j>0 && j<=numV))
156 {
157 if ( (Edge[i-1][j-1] != 0) && (Edge[i-1][j-1] == MaxWeight) )
158 {
159 Edge[i-1][j-1] = w; //更改對應(yīng)的行和列的權(quán)值
160 }
161 else
162 {
163 cout << "\t邊已經(jīng)存在!" << endl;
164 //exit (0);
165 }
166 }
167 else
168 {
169 cout << "\t插入位置錯誤!" <<endl;
170 //exit (0);
171 }
172
173}
174
175//刪除一條邊的算法
176void AdjMWGraph::DeleteE()
177{
178 int i,j;
179 cout << "\n 請輸入要刪除的邊的起點和終點(vi,vj):";
180 cin >> i >> j;
181 if ((i>0 && i<=numV) && (j>0 && j<=numV)) //判斷起點各終點是否存在
182 {
183//判斷是否是對角線上的點,判斷是否是邊已經(jīng)存在
184 if(( i != j ) && (Edge[i-1][j-1] != MaxWeight) )
185 {
186 Edge[i-1][j-1] = MaxWeight; //對應(yīng)的行和列權(quán)值置零
187
188 }
189 else
190 {
191 cout << "\t刪除的邊不存在!" << endl;
192 //exit (0);
193
194 }
195 }
196 else
197 {
198 cout << "\t刪除位置錯誤!" <<endl;
199 //exit (0);
200 }
201
202}
203
204int main(int argc, char* argv[])
205{
206 AdjMWGraph G ;
207 int n,e;
208 int k;
209
210 do
211 {
212 cout << "\n\t 1.創(chuàng)建圖" <<endl;
213 cout << "\n\t 2.插入一條邊" <<endl;
214 cout << "\n\t 3.刪除一條邊" <<endl;
215 cout << "\n\t 4.退出" <<endl;
216 cout << "\n\t ==========================" << endl;
217 cout<< "\n\t請輸入您的選擇(1,2,3,4):";
218 cin >> k;
219
220 switch(k)
221 {
222
223 case 1:
224 {
225 cout << "\n 請輸入圖的總頂點數(shù)和總邊數(shù)（n,e=?）：";
226 cin >> n >> e ;
227 G.CreatG(n,e);
228 G.PrintOut();
229 cout << "最小生成樹如下";
230 cout << "共有" << n-1 << "條邊" ;
231 G.Prim();
232 }break;
233
234 case 2:
235 {
236 G.InsertE();
237 G.PrintOut();
238 G.Prim();
239
240 }break;
241
242 case 3:
243 {
244 G.DeleteE();
245 G.PrintOut();
246 G.Prim();
247
248 }break;
249 case 4:
250 exit (0);
251 }
252 }while( k >0 && k <5 );
253 return 0;
254}
255
五.心得:
這次實驗我把無向圖改成有向圖后,對實驗中給出的生成最小生成樹的Prim算法感到費解這里只能說說在實現(xiàn)插入和刪除時的心得.在創(chuàng)建圖時我在程序中加入判斷語句,因為在給邊權(quán)時如果頂點不存在會造成鎖死,嚴(yán)重影響調(diào)試.在創(chuàng)建和插入中主要判斷的是:1,頂點是否越界.2邊是否已經(jīng)存在.3插入位置是否是矩陣的對角線.在刪除中判斷1,頂點是否越界.2邊是否已經(jīng)存在.對于Prim算法的求最小生成樹的思想能夠理解,但對于算法的實現(xiàn)不甚理解.希望老師在下次實驗時講解.
六.使用說明
程序名為No5.exe運行環(huán)境為DOS,執(zhí)行后顯示:
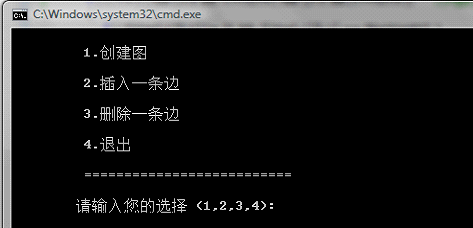
在" 請輸入您的選擇(1,2,3,4):"后輸入數(shù)字選擇執(zhí)行的功能.
測試結(jié)果:
- 選擇1.輸入如圖:
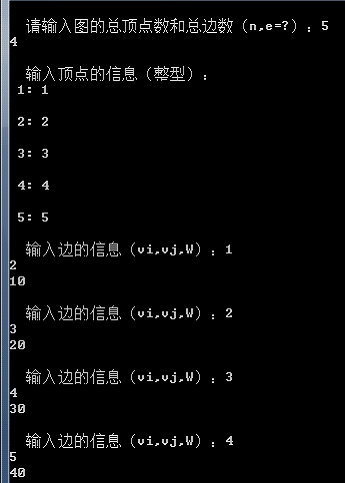
得
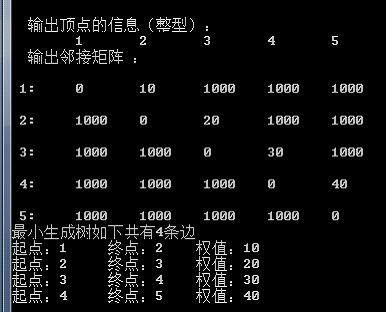
- 選擇2操作如圖:
再次操作
再次操作
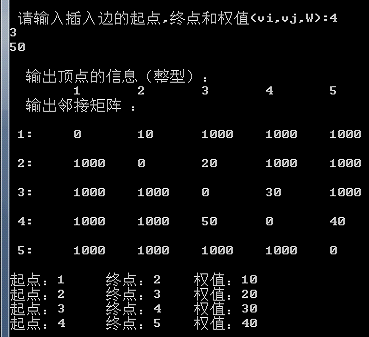
3)選擇3操作如圖
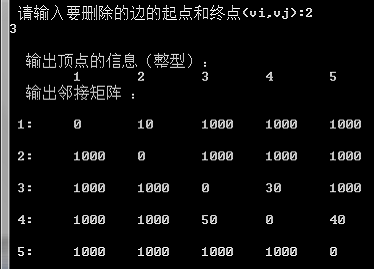
再次操作
再次操作
4) 選擇4或輸入非"1,2,3"的數(shù)字
七.調(diào)試過程
本程序主要對插入邊操作功能進行調(diào)試..
- 將光標(biāo)移置Graph.cpp文件的void AdjMWGraph::InsertE()的第一條語句處Ctrl+F10開始單步調(diào)試
- 選擇1.后創(chuàng)建圖
再選擇2.
-
這時Debugger仍停留在void AdjMWGraph::InsertE()的第一條語句上.在中輸入numV, I, j ,i!=j ,Edge[i-1][j-1]進行觀察.F10單步至cin >> i >> j >> w;語句.然后在DOS窗口輸入4,3,55回車.
這時Debugger仍停留在if ( ( i != j ) && (i>0 && i<=numV) && (j>0 && j<=numV))處.可以在監(jiān)視1窗口中看到 i != j的值為true,即可以步入if()語句.
-
在監(jiān)視窗口1中輸入: (Edge[i-1][j-1] == MaxWeight), (Edge[i-1][j-1] != 0)進行觀察,F10單步調(diào)試,這時Debugger停留在if ( (Edge[i-1][j-1] != 0) && (Edge[i-1][j-1] == MaxWeight) )語句處,同時在監(jiān)視窗口1中可以看到(Edge[i-1][j-1] == MaxWeight), (Edge[i-1][j-1] != 0)都為真,即可以步入if()語句中.F10后可以看到Edge[i-1][j-1]值已經(jīng)變?yōu)?/span>55
-
F10單步調(diào)試到結(jié)束可以在DOS窗口中看到矩陣中相應(yīng)的位置已經(jīng)改變
Shift+F5退出調(diào)試,完成調(diào)試演示.