游戲中有點擊障礙點,人物走到離障礙物最近點的算法。我這給一個簡單的算法,這個問題可以復雜化,另外這個問題應該由客戶端來完成。
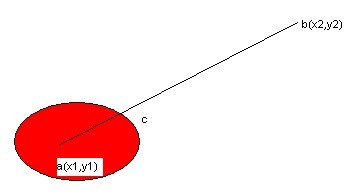
如圖,玩家在b點,點擊了a點,a在一個障礙區(紅色,玩家只能在障礙區外移到)。這時候玩家應該走到c點,我們就需要計算出c點,一個簡單的數學題,用什么語言都沒幾行代碼,我就用erlang寫一下。
障礙物通常都不規則的,我們只能從a點開始一個個點測試,直到不是障礙點,也就是x自增,y=x*tan(A),然后測試這個點,地圖數據都是靜態的數據,方便測試,這里就寫死一個x為障礙結束的地方作為障礙檢測函數。
我們還需要一個記錄表示點,tan函數在erlang中是有的,但其實可以不用,我們就直接要一個比值,但需要一個向上取整的函數,據說是round函數,但測試一下,不行,難道是因為不是最新otp
D:\NetBeanPj\mytest\src>erl
Eshell V5.8.1.1 (abort with ^G)
1> round(1.2).
1
所以這里我們要寫的一個輔助函數,最后就是我們的重點,取最近點,用一個列表解析就夠了,剩下的就看具體實現吧,還可以寫個測試函數,這次就不寫成單元測試了。好的我們看代碼:
-module(nearst_point).
-export([ceil/1, is_barrier/1, nearst_point/2]).
-export([p1/0, p2/0, test_1/0]).
%% 一個點
-record(point,{
x,
y
}).
%% 向上取整
ceil(Num) ->
Num1 = round(Num),
case Num1 >= Num of
true ->
Num1;
false ->
Num1+1
end.
%% 判斷是否是障礙物
is_barrier(Point) ->
Point#point.x =/= 5 .
%% 查找最近點
nearst_point(Pointa,Pointb) ->
Tan = (Pointa#point.x - Pointb#point.x)/(Pointa#point.y - Pointb#point.y),
case Pointa#point.x > Pointb#point.y of
true ->
MaxX = Pointa#point.x,
MinX = Pointb#point.x;
false ->
MaxX = Pointb#point.x,
MinX = Pointa#point.x
end,
try
[
begin
Point = #point{
x = X,
y = ceil(X*Tan)},
case is_barrier(Point) of
true ->
ok;
false ->
throw(Point)
end
end|| X <- lists:seq(MinX, MaxX)]
catch
throw: Point ->
io:format("~p", [Point]),
Point
end.
%% 下面函數測試用,可以改成單元測試,這里就免了
p1() ->
#point{
x = 1,
y = 9}.
p2() ->
#point{
x = 15,
y = 25}.
test_1() ->
nearst_point(p1(),p2()).
編譯和測試
2> c(nearst_point).
{ok,nearst_point}
3> nearst_point:test_1().
{point,5,5}{point,5,5}
4>
我們的測試如預期的在5那個點得到,好像有個小問題,怎么這個點輸出了兩次?哦,這不是問題,一個點是代碼里的io輸出的,一個點是返回給shell,shell的輸出,看來寫代碼的人太懶,疑惑也會增多啊。在nearst_point中用到了一個小技巧,就是用throw來跳出循環(這個在erlang中還是挺有意思),這次到這,應該說寫的很基礎很難看。下次會來點有意思的,歡迎大家學習erlang。