Change Dir

Logistic Regression——用線解決問題

LR一般用于預測二分類問題，即yes no和0\1問題，我們構建了X(設備屬性和行為屬性)，我們需要預測Y(是否異常)，而反作弊項目中，我們需要預測的就是設備作弊or正常,即0\1問題。選擇LR一個很重要的原因是我們相信X和Y是有聯系的，不同的類型的Y會有不同的X表現。

而X和Y是否有線性關系？ 普通線性回歸(Ordinary Linear Regression)是否就能滿足需求？我們需要先論證這個問題，我們看一下普通線性回歸，模型是這樣的：

在線性回歸中，隨機誤差項服從正態分布。這也意味著回歸的Y值是個連續變量，不能是0\1這樣的binary變量。另外一個解釋就是線性回歸對響應變量Y的要求是有常數方差，這也限定了Y的分布，就比如二項分布的Y就沒有常數方差。這也正符合我們常規的閱讀理解，回歸用于定量分析，更多的在擬合和預測量上，而分類是個定性分析。正因為OLR的做法限制太多，因此有了通用線性回歸的方法（General Linear Regression），通用方法的思路就是尋求一個轉換函數g來作用于輸入變量X，從而擺脫對Y的分布限制。具體表現為

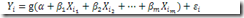
下面兩張圖對比了線性回歸和邏輯回歸數據的特點，也說明了如果用線性回歸來分類binary數據是一個什么樣的效果。

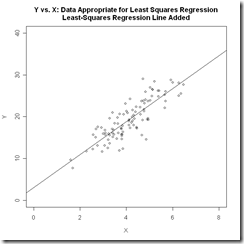
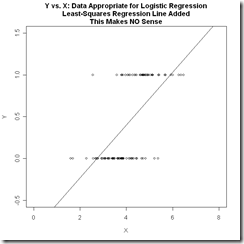
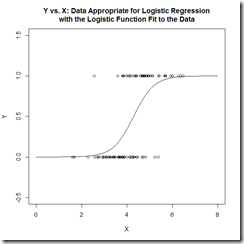
其實比較樸素的理解就是，我們把要分類的數據劃分為0和1兩類，那么數據其實是會以中間這幅圖的形式分布的，必然存在一個平面（直線）把數據劃分。而我們希望找到一個判別函數能完成區分，顯而易見的是直線無法完成這個事情。

面對線性回歸的劣勢，我們理解回歸的問題在于無法對公式（1）的結果做0\1劃分，線性回歸的方法做分類，就是要求

而邏輯回歸作為GLR的一個特殊情況，定義了一函數f()，這個函數可以將Y做0\1處理，從而使線性回歸變得有意義。而邏輯回歸的做法就是找到了這樣一個函數，這個函數也叫logit函數

其中我們把p等價于原來的 ，解釋一下就是p代表Y=1的概率，標準說法p是Y=1時Y的期望。然后把這個p替換掉就得到了

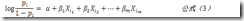
目標是求解，于是

這里就不是一個線性函數了，上面提到的公式（2）對應的曲線上面最右邊的圖——可以看到p的函數曲線，這樣的劃分對于0\1數據的分類是非常合適的。

那么一個問題就隨之而來，logit函數是怎么來的？要想知道答案，我們需要先分析一下這個形式，我們定義這個形式為“優勢”（odds），odds有時候也叫做“幾率”，odds的函數形式其實是下面左圖的樣子，而logit函數的形式是右圖的樣子

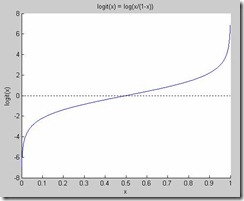
odds的理解其實要結合概率的思想，我們認為一個事件發生的概率是p，那么不發生的概率就是1-p，而odds表達的就是事件發生與不發生（或者一個標注yes 或者no）的幾率，比如一個事情發生的概率是0.9，而不發生是0.1，那么odds（發生）=0.9/0.1=9，而odds(不發生)=0.1/0.9=0.1111...。這說明一種事物相比較時的優勢，但是這個優勢在形式上非對稱，這樣是不完美的，也是難于理解的，畢竟對于一個0-1之間的概率比較，結果卻在0-∞之間。而可以看出logit函數是把odds對數化后得到的一個對稱的美妙的曲線，擁有我們想要的所有性質，并且解決了OLR所限制的問題，而且由公式（3）我們也能看到，logit函數使結果限定在0-1之間，且是輸入變量X的線性表示。

最后當我們計算出p，我們就能確定分類，比如p>0.5時 y=1，而p<0.5時y=0。于是這樣的分類任務就結束了。不過我們再看看模型，似乎忘記了什么，我們可以從數據集里得到X和Y，但是對于α和β以及ε的值（參數值），我們需要獲取到。而這才是LR作為機器學習方法最關鍵的一個部分。

我們假設數據集有n個數據樣本，且n大于估計的參數的個數，于是我們令

我們用β表示整個參數向量，那么原來的表達式可以寫為Y=X*β。類似最小二乘法的思路，我們有下面的推斷

其實如果把目標約定為計算β,那么問題也就被歸約為一個參數估計問題，而我們最常用的方法就是極大似然估計法。這里不具體介紹MLE，換種角度我們從頭開始設計這個分類器。

之前考慮的點我們簡化了分析，我們理所當然的認為X特征向量彼此是同等重要的，而事實往往不是這樣，因此模型需要加入一個權重影響因子，也就是LR模型被擴展為Weighted Logistic Regression，因為目標是計算公式（5），加入權重后，我們把評估公式（5）的做法替換為去評估

這里就涉及一個問題：權重具體是個什么定義？權重W是個對角矩陣，其對角元素即每個特征項的權重值，而這個權重定義為預測變量的標準差。此時我們回到一個基本問題，LR用來預測二類問題，而我們一般假設我們的預測變量Y是服從二項分布的即，那么方差，更特殊的，對于單次試驗是伯努利分布，所以有，而這個即我們對于預測變量Y的估計值，形如公式（4），換用現在對β的定義就是，回到公式（6）中，我們新引入的變量U即表示為，其中后面這個加項我們這么理解：分子是一個預測誤差項，而分母是我們定義的權重，這樣一個比值縮放了正確分類的大方差樣本點和小方差樣本點對結果的影響。另外需要引入的一個概念是嶺回歸（Ridge Regression），源于一些預測變量y可能是線性相關的，那么這會導致是奇異矩陣，會導致無窮解，因此在帶求解的公式（6）的基礎上，為可逆矩陣引入一個常量對角矩陣，公式變為

其中是小常量，而I是單位矩陣。這樣做避免了對奇異矩陣求逆，但是帶來了問題就是對預測變量結果的偏置，導致目標問題發生了小小的變化。多種方法可以幫助我們尋找一個好的，這里就不具體展開了，具體參考資料即可。

最后就是算法實現了，為了避免復雜的矩陣求逆，我們把形式變一下，將公式（7）轉換為求解這樣一個線性系統

其中，。可以看出，算法的輸入是特征矩陣X和U（間接得到），輸出是β。求解線性系統的算法有很多，其中共軛梯度算法是非常有效的算法，下面左圖描述了共軛梯度算法的實現偽代碼。

共軛梯度：

IRLS：

其中值得一提的是共軛梯度算法中的“is large enough”或者維基上說的“sufficiently small”有多種判斷方式，具體這里就不列出了，可以看參考資料[2]。右圖是迭代重加權最小二乘法，用于最終求解β。

我在github上放了一個《machine learning in action》中的LR算法的python實現，對于β的求解使用的是梯度下降法，可以參考https://github.com/changedi/mlmlml/blob/master/LogisticRegression/logRegres.py，而關于梯度下降等最優化算法，我想還是單獨開一篇去介紹比較合適。至此，LR的基本介紹基本就結束了。

文中除流程圖外，其他截圖取自ref[2]，特此聲明。

References:

[1] http://logisticregressionanalysis.com/86-what-is-logistic-regression/

[2] http://www.omidrouhani.com/research/logisticregression/html/logisticregression.htm

[3] 《統計學習方法》，李航

[4] Logit Models for Binary Data, G. Rodriguez, 2007

[5] http://zh.wikipedia.org/wiki/%E5%85%B1%E8%BD%AD%E6%A2%AF%E5%BA%A6%E6%B3%95

[6] http://cnx.org/content/m45285/latest/

posted on 2014-08-05 09:38 changedi 閱讀(4326) 評論(1)  編輯  收藏 所屬分類: 機器學習 、數學