影響空間規模的幾種數據存儲結構
正文
所謂數據存儲結構,就是數據的元素與元素之間在計算機中的一種表示,它的目的是為了解決空間規模問題,或者是通過空間規模問題從而間接地解決時間規模問題。我們知道,隨著輸入的數據量越來越大,在有限的內存里,不能把這些數據完全的存下來,這就對數據存儲結構和設計存儲的算法提出了更高的要求。
本文將介紹幾種存儲結構,分別為鏈式結構、樹形結構、圖結構以及矩陣結構。
第一節 鏈式存儲結構
所謂鏈式存儲結構,一般就是用一個頭指針指向鏈表的第一個節點,如果你要增加新的存儲元素時,只需在已有節點的后面插入新結點即可。
鏈表通常有單鏈表、雙鏈表、循環鏈表。在這,我只介紹單鏈表,雙鏈表和循環鏈表只是單鏈表的拓展罷了。下圖就是一個簡單的單鏈表圖示。

單鏈表的類型描述如下代碼:
- typedef char DataType;
- typedef struct node{
- DataType data;
- struct node *next;
- }ListNode;
- typedef ListNode *LinkList;
- ListNode *p;
- LinkList head;
- 附注:
- ① LinkList和ListNode *是不同名字的同一個指針類型(命名的不同是為了概念上更明確)
- ② LinkList類型的指針變量head表示它是單鏈表的頭指針
- ③ ListNode *類型的指針變量p表示它是指向某一節點的指針
下面我們來看單鏈表的操作:創建節點、增加節點、刪除節點、查詢、修改。
1.創建節點:聲明一個節點并為其申請一段內存空間,此節點有數據域和指針域。
- node = (struct List *)malloc(sizeof(struct List));
2.增加節點:插入節點,分為頭插入、尾插入和非頭尾插入。
①. 在表頭插入節點,
如圖
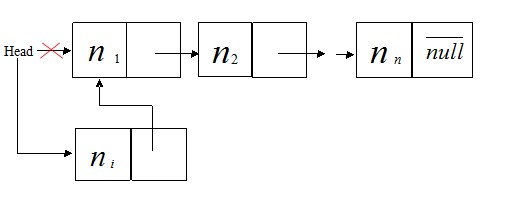
插入頭節點的代碼如下:
- if(p == head)
- {
- struct list *s = NULL;
- s = (struct list *)malloc(sizeof(struct list));
- s->DataNumber = data;
-
-
- s->next = p;
- head = s;
- }
②. 在表尾插入節點,
如圖
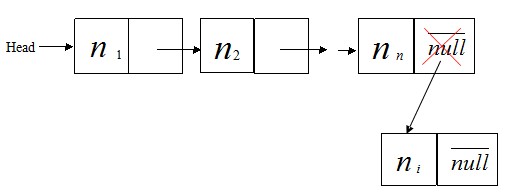
插入尾節點的代碼如下:
- if(p->next == NULL)
- {
- struct list *s = NULL;
- s = (struct list *)malloc(sizeof(struct list));
- s->DataNumber = data;
-
-
- p->next = s;
- s->next = NULL;
- }
③. 在表中插入非頭尾節點,
如圖
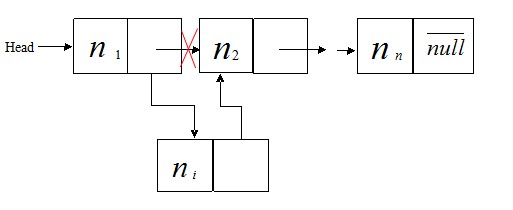
插入非頭尾節點的代碼如下:
- struct list *s = NULL;
- s = (struct list *)malloc(sizeof(struct list));
- s->DataNumber = data;
-
-
- s->next = p;
- q->next = s;
3.刪除節點:分為刪除頭結點,刪除尾節點,刪除頭尾節點。
①. 刪除表頭結點,
如圖
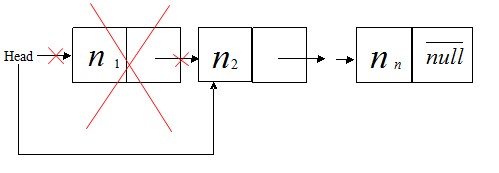
刪除頭結點的代碼如下:
- if(p == head)
- {
- head = p->next;
- }
②. 刪除表尾節點,如圖
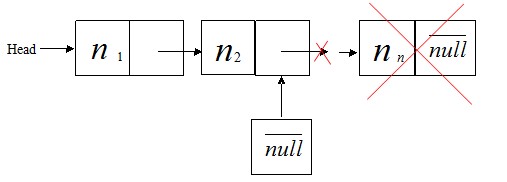
附注說明:上圖中刪完尾節點之后,新鏈表的尾節點下標應為n-1。不過由于作圖時只做了尾節點,故用圖中的n2節點代替。
刪除尾節點的代碼如下:
- if(p->next == NULL)
- {
- q->next = NULL;
- }
③. 刪除非頭尾節點,如圖

刪除非頭尾節點的代碼如下:
4.查詢節點:在鏈表中找到你想要找的那個節點。此操作是根據數據域的內容來完成的。查詢只能從表頭開始,當要找的節點的數據域內容與當前不相符時,只需讓當前節點指向下一結點即可,如此這樣,直到找到那個節點。
附注:此操作就不在這用圖和代碼說明了。
5.修改節點:修改某個節點數據域的內容。首先查詢到這個節點,然后對這個節點數據域的內容進行修改。
附注:同上
ok,鏈表的幾種操作介紹完了,接下來我們來總結一下鏈表的幾個特點。
鏈式存儲結構的特點:
1.易插入,易刪除。不用移動節點,只需改變節點中指針的指向。
2.查詢速度慢:每進行一次查詢,都要從表頭開始,速度慢,效率低。
擴展閱讀
鏈表:http://public.whut.edu.cn/comptsci/web/data/512.htm
第二節 樹形存儲結構
所謂樹形存儲結構,就是數據元素與元素之間存在著一對多關系的數據結構。在樹形存儲結構中,樹的根節點沒有前驅結點,其余的每個節點有且只有一個前驅結點,除葉子結點沒有后續節點外,其他節點的后續節點可以有一個或者多個。
如下圖就是一棵簡單的樹形結構:
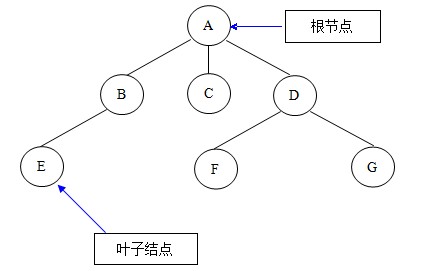
說到樹形結構,我們最先想到的就是二叉樹。我們常常利用二叉樹這種結構來解決一些算法方面的問題,比如堆排序、二分檢索等。所以在樹形結構這節我只重點詳解二叉樹結構。那么二叉樹到底是怎樣的呢?如下圖就是一顆簡單的二叉樹:
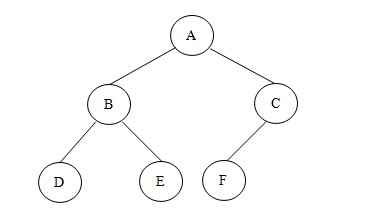
附注:有關樹的概念以及一些性質在此不做解釋,有意者請到百科一覽。
二叉樹的類型描述如下:
- typedef struct tree
- {
- char data;
- struct tree * lchild, * rchild;
- }tree;
二叉樹的操作:創建節二叉樹,創建節點,遍歷二叉樹,求二叉樹的深度。
1.創建二叉樹:聲明一棵樹并為其申請存儲空間。
- struct tree * T = NULL;
- T = (struct tree *)malloc(sizeof(struct tree));
2.創建節點:除根節點之外,二叉樹的節點有左右節點之分。

創建節點的代碼如下:
- struct tree * createTree()
- {
- char NodeData;
- scanf(" %c", &NodeData);
- if(NodeData == '#')
- return NULL;
- else
- {
- struct tree * T = NULL;
- T = (struct tree *)malloc(sizeof(struct tree));
- T->data = NodeData;
- T->lchild = createTree();
- T->rchild = createTree();
- return T;
- }
- }
3.遍歷二叉樹:分為先序遍歷、中序遍歷、后續遍歷。
①.先序遍歷:若二叉樹非空,則依次執行如下操作:
(1) 訪問根結點;
(2) 遍歷左子樹;
(3) 遍歷右子樹。
如圖:
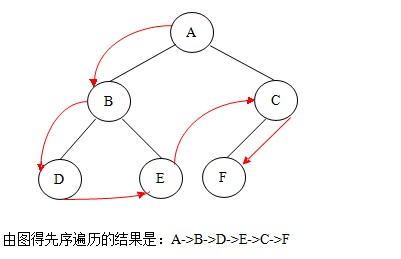
先序遍歷的代碼如下:
- void PreTravser(struct tree * T)
- {
- if(T == NULL)
- return;
- else
- {
- printf("%c",T->data);
- PreTravser(T->lchild);
- PreTravser(T->rchild);
- }
- }
②.中序遍歷:若二叉樹非空,則依次執行如下操作:
(1)遍歷左子樹;
(2)訪問根結點;
(3)遍歷右子樹。
如圖:
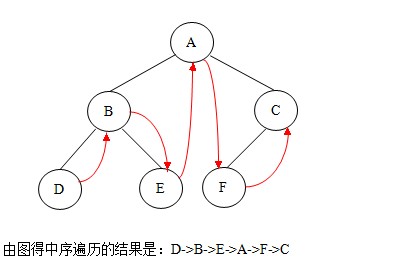
中序遍歷的代碼如下:
- void MidTravser(struct tree * T)
- {
- if(!T)
- {
- return;
- }
- else
- {
- MidTravser(T->lchild);
- printf("%c",T->data);
- MidTravser(T->rchild);
- }
- }
③.后續遍歷:若二叉樹非空,則依次執行如下操作:
(1)遍歷左子樹;
(2)遍歷右子樹;
(3)訪問根結點。
如圖:

后續遍歷的代碼如下:
- void PostTravser(struct tree * T)
- {
- if(!T)
- return;
- else
- {
- PostTravser(T->lchild);
- PostTravser(T->rchild);
- printf("%c->",T->data);
- }
- }
4.求二叉樹的深度:樹中所有結點層次的最大值,也稱高度。
二叉樹的深度表示如下圖:
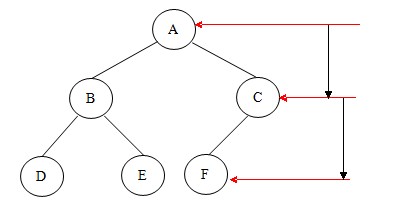
求二叉樹深度的代碼如下:
- int treeDeepth(struct tree * T)
- {
- int i, j;
- if(!T)
- return 0;
- else
- {
- if(T->lchild)
- i = treeDeepth(T->lchild);
- else
- i = 0;
-
- if(T->rchild)
- j = treeDeepth(T->rchild);
- else
- j = 0;
- }
- return i > j? i+1:j+1;
- }
好了,二叉樹的幾種操作介紹完了。
拓展閱讀
二叉樹:http://student.zjzk.cn/course_ware/data_structure/web/DOWNLOAD/%CA%FD%BE%DD%BD%E1%B9%B9%D3%EB%CB%E3%B7%A82.htm
赫夫曼編碼:http://blog.csdn.net/fengchaokobe/article/details/6969217
第三節 圖型存儲結構
所謂圖形結構,就是數據元素與元素之間的關系是任意的,任意兩個元素之間均可相關,即每個節點可能有多個前驅結點和多個后繼結點,因此圖形結構的存儲一般是采用鏈接的方式。圖分為有向圖和無向圖兩種結構,如下圖
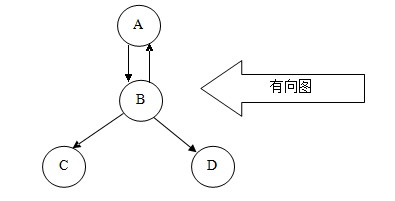
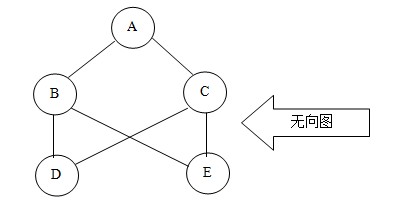
通過圖,我們可以判斷兩個點之間是不是具有連通性;通過圖,我們還可以計算兩個點之間的最小距離是多少;通過圖,我們還可以根據不同的要求,尋找不同的合適路徑。
1.圖的結構有好幾種,在實際應用中需根據具體的情況選擇合適的結點結構和表結構。常用的有數組結構、鄰接表。
①.數組結構
數組結構的類型描述如下:
- typedef char VertexType;
- typedef int EdgeType;
- #define maxvex 100 /***頂點的最大個數***/
-
- typedef struct
- {
- VertexType vexs[maxvex];
- EdgeType arc[maxvex][maxvex];
- }Mgraph;
附注:當前圖為無向圖時,圖中某兩個頂點VA和VB構成一條邊時,其權值可表示為EdgeType arc[VA][VB];當前圖為有向圖時,圖中某兩個頂點VA和VB構成一條邊時,并且是由VA指向VB,其權值可表示為EdgeType arc[VA][VB],如果是由VB指向VA,其權值可表示為EdgeType arc[VB][VA]。
②.鄰接表
鄰接表的類型描述如下:
- typedef char VertexType;
- typedef int EdgeType;
-
- typedef struct EdgeNode
- {
- int adjvex;
- EdgeType weight;
- struct EdgeNode *next;
- }EdgeNode;
-
- typedef struct VertexNode
- {
- VertexType data;
- EdgeNode * firstedge;
- }VertexNode,AdjList[MAXVEX];
-
- typedef struct
- {
- AdjList adjList;
- int numVertexes,numEdges;
- }GraphAdjList;
2.圖的遍歷:從圖中的某一節點出發訪問圖中的其余節點,且使每一節點僅被訪問一次。圖的遍歷算法是求解圖的連通性問題、拓撲排序和求路徑等算法的基礎。圖的遍歷分為深度優先遍歷和廣度優先遍歷,且它們對無向圖和有向圖均適用。
①. 深度優先遍歷
定義說明:假設給定圖G的初態是所有頂點均未曾訪問過。在G中任選一頂點V為初始出發點,則深度優先遍歷可定義如下:首先訪問出發點V,并將其標記為已訪問過;然后依次從V出發搜索v的每個鄰接點W。若W未曾訪問過,則以W為新的出發點繼續進行深度優先遍歷,直至圖中所有和源點V有路徑相通的頂點(亦稱為從源點可達的頂點)均已被訪問為止。若此時圖中仍有未訪問的頂點,則另選一個尚未訪問的頂點作為新的源點重復上述過程,直至圖中所有頂點均已被訪問為止。
深度遍歷過程如下圖:
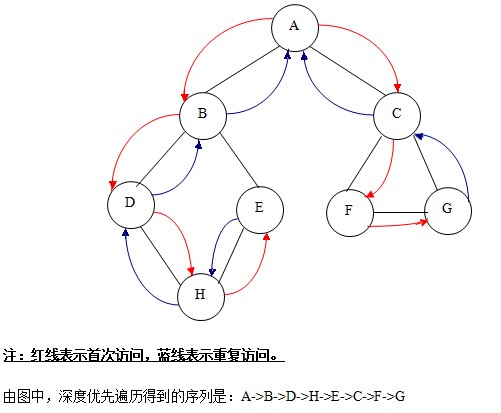
②. 廣度優先遍歷
定義說明:假設從圖中某頂點V出發,在訪問了V之后一次訪問V的各個未曾訪問過的鄰接點,然后分別從這些鄰接點出發依次訪問它們的鄰接點,并使“先被訪問的頂點的鄰接點”先于“后被訪問的頂點的鄰接點”被訪問,直至圖中所有已被訪問的頂點的鄰接點都被訪問到。若此時圖中還有頂點未被訪問,則另選圖中一個未曾被訪問的頂點作為起始點,重復上述過程,直至圖中所有頂點都被訪問到為止。換句話說,廣度優先遍歷圖的過程是以V為起點,由近至遠,依次訪問和V有路徑相同且路徑長度為1,2,...的頂點。
廣度遍歷過程如下圖:
作者:csh624366188 發表于2012-4-9 22:54:15
原文鏈接