量化項目管理案例：缺陷趨勢預測利器（1）

　不知身為軟件工程師的你，在寫代碼時是不是有過這樣的經歷：一方面對自己寫的代碼信心滿滿，一方面又非常希望知道自己開發的代碼的質量到底多高。如果代碼真的沒被測出bug來或者測出的bug較少時，反而有點擔心——會不會還有隱藏的更深的bug沒被發現？或者身為測試工程師的你，可能比開發人員擔心的會更多：這些代碼該不該再繼續測試了？怎么就能斷定當前的版本算是通過驗收標準了，繼而可以被客戶和用戶認可？是不是就可以把這個版本交付使用了呢？

　　--------------------------------------------------------------------------------

　　相信這是很多開發和測試人員都曾經經歷過的。無論是開發人員、測試人員，還是項目經理、高層管理人員，都已經為版本的交付日以繼夜的加班工作，可不能在交付的時刻功虧一簣。打擊心情不說，加班加點不說，而且，誰該來為可能的返工和無休無止的變更買單呢。

　　所以，軟件版本在發布時需要有一個判定的標準——沒有預先定義的判定標準，就無法去判斷版本是否已經達到了客戶的要求。不進行判斷，或者是錯誤的判斷，都很有可能會造成該項目資源安排的不合理，甚至造成資源的浪費，那么不管是精神上還是體力上，甚至進度上、成本上，都會給項目團隊帶來不小的打擊。

　　CMMI四級的一個要求是量化的管理項目（詳見量化項目管理QPM中文版）。映射到缺陷預測活動中，也就是量化的管理缺陷。量化的退出標準就是將類似“這個版本是否能夠通過”這樣的問題，形象地轉變為“已經測出的bug數是否已經足夠多，遺留的bug是否已經少到不會影響軟件的交付”等等這樣的表述。這樣，無論是理解上還是判斷上都更加容易，版本發布標準也就變得不難理解了。

　　在決定發布版本之前，需要去統計這樣幾件事：我們已經發現了多少個bug；用量化的方法進行管理時，我們還有多少個bug沒有發現；我們統計到的未發現的bug數是否能達到客戶的要求；如果無法滿足客戶的要求，那我們至少還需要發現多少個bug。當這一系列問題都解決了以后，開發、測試人員是終于可以“收”工拿項目獎，還是需要返工加班、繼續努力，也就一目了然了。

　　知道了要做什么，接下來要考慮的就是“怎么做”。出于這樣的原因，方正國際軟件有限公司（以下簡稱方正國際）幾年來一直都在內部實施著利用統計學的原理對軟件缺陷進行管理和監控。用統計學的方法監控和預測缺陷的發展情況，從而對發現的缺陷進行管理，確定還未發現的缺陷情況、為了按時交付每一個階段應當發現的缺陷情況，以此相應調整測試工作的時間和進度。

　　這就是方正國際近兩年來一直在內部實施的基于Gompertz模型的缺陷預測與管理，以及在此基礎上開發的缺陷預測與管理的工具。在已經采集到的多個項目數據的基礎上，現在該工具已經在公司內部使用。應用這個工具，讓測試人員在測試初期就對自己大致的工作量有了比較準確的估計，并對測試的每個階段發現的bug實施分析和監控；根據預實對照的目標達成情況來調整開發、測試的進度；而且在最終交付時，給客戶一個高質量的、可靠的工作產品。簡單用個例子來說明吧。在項目A還未進入但即將進入測試階段時，測試經理就會根據歷史的情況、經驗等方法，估計出進入測試階段后的第一周，大概可以發現多少件缺陷；同樣，再估計出版本交付時可能出現的缺陷數目，以及版本交付后會出現的缺陷的數目。利用這三個數據的信息，就大致可以得到：要達到預定的目標，在進入測試階段后，每周、甚至每天大概需要發現多少缺陷。以此為依據，測試經理就可以對團隊中的測試人員的任務進行分配、對工作進行評價。當然，這僅僅是Gompertz模型使用的場景之一。

　　統計學是很強大的，統計學知識的應用也是很廣泛的。那么，在缺陷預測中的統計學原理，或者說是理論依據是什么呢？基于Gompertz模型的缺陷預測工具到底是怎樣對測試活動和質量進行監控的呢？接下來，我們會逐步與大家分享。

　　未完待續......

趨勢預測、基于時間信息的預測相關基礎知識

　　在展開Gompertz模型趨勢預測的說明前，首先給關注統計學知識在軟件行業應用的網友介紹趨勢預測的基礎知識。

　　如何理解預測技術呢？簡單來說，預測（prediction）是根據事物發展的歷史資料及當前情況，運用一定的理論和方法，對未來趨勢做出的一種科學推測。再簡單點，就像傳說中或是童話里的占卜師一樣，當你想知道將來的事情時，你需要告訴占卜師你的出生情況，他就能將你的一生預測出來。不同的是，他只能告訴你，你的一生是順利或是不順，或再詳細點告訴你可能在哪段時間會發生不尋常的事情；而我們所說的預測技術卻可以詳細到周，甚至詳細到天。當然，這里還有個本質的區別，那就是我們這里說的預測是有科學基礎的，而占卜師的預測只是常常出現在童話里或者傳說中罷了。

　　預測技術的應用主要針對未來的趨勢，即是經常講的趨勢預測？這里我們也來個“顧名思義”。“趨勢”一詞在詞典里的解釋是“事物發展的動向”，也就是會呈現出某種規律。簡單點，某一事物未來是好是壞，是多是少，是升是降，或者先好后壞，先多后少，先升后降等等，也就是對未來進行預測。再用上面的例子來說明，小李急切地想知道自己的未來，并求助于占卜師，而占卜師則預測到他在40歲時會有場災禍，那么恐怕小李緊接著要問的就是“我該怎樣做才能化解我的災禍”。趨勢預測就是要解決類似的問題。預測并不是最終目的，而是一種手段，當預測到的趨勢不符合規定的標準時，就應當及時采取措施來進行調整或緩解，這也是趨勢預測的目標之一，通過分析預測的結果，揭發它的發展趨勢，從而使得人們能夠盡早地發現問題，或得到一個科學論斷和標準。現在從童話回到現實中來。在軟件領域，缺陷的趨勢預測是預測技術應用較為廣泛的領域之一，它是利用統計的手段來預測產品或解決方案中的遺留缺陷、測試階段的單位時間內應當查出的缺陷等，因此對軟件質量的提高和測試階段的管理起著重要作用。

　　在軟件領域中，一條重要的原則就是“do it right the first time”。這條原則告訴軟件行業的工作人員：應當在第一次就將事情做對。然而實際中的情況是，軟件開發完成后總還是存在缺陷，所以才需要測試，才需要品質保證；考慮業務的復雜性、開發工具的更新、需求的不穩定性、開發人員的能力經驗欠缺等因素，幾乎不能在第一次就將事情完全的做對，取而代之的是不斷的驗證、測試、修改再確認，才能最終確保軟件產品或服務的正確性。然而有一件事可以確定，某個軟件系統中的缺陷數目應當是一定的，隨著軟件系統生命周期的推進，發現的缺陷數應當由少到多，再從多到少并趨近于零。那么，如果無法做到“第一次將事情做對”，也要“盡早將事情做對”，在缺陷可能帶來巨大的風險之前，就將它“扼殺在搖籃里”。如果沒有預測，不知道未來趨勢，也就無法判斷當前處于怎樣的狀態下，更無法知道，在當前階段，是不是已經有缺陷遺留到了下一階段。這一點其實很容易理解，本來需要在2周內每天完成30項任務，但第一周只完成了10項，那接下來的一周內就需要加班加點完成剩下的50項任務；如果未能完成，那就可能導致無法交付任務，帶來足以讓你后悔的結果。

成長曲線

　　終于要介紹到預測方法啦。有了前面兩篇文章的基礎，大家應該都對預測有了認識。還是那句話，知道了要做什么，接下來就該想要“怎么做”。明白了預測的重要性，那就該去想想，怎么去預測？不過別心急，我們一步一步來，這篇文章會介紹預測工具的基礎知識——成長曲線。

　　什么是成長曲線？成長曲線就是描繪觀測樣本從初始階段不斷發展壯大所經歷的全部過程的曲線。在軟件領域的成長曲線的過程中，要觀測的樣本值會經歷萌芽、發展、穩定等階段。成長曲線在很多方面都有應用，比如在報紙上、經濟類刊物上常常能看到的經濟成長曲線、品牌成長曲線；再比如細心的媽媽都會把寶寶出生后的成長情況記錄下來，繪成兒童成長曲線等等。

　　在軟件領域中同樣有成長曲線，軟件領域中的成長曲線反映了軟件系統中的要觀測的某個屬性隨著各種因素（如時間、成本等）變化發展的情況。成長曲線可以擬合事物發展的趨勢，曲線擬合（Curve fitting）就是用連續曲線近似地刻畫或比擬平面上離散的點表示的坐標之間的函數關系的一種數據處理方法。在數值分析中，曲線擬合就是用解析表達式逼近離散數據，即離散數據的公式化，就是選擇適當的曲線類型來擬合觀測數據，并用擬合的曲線方程分析兩變量間的關系。

　　接著回到軟件領域中的成長曲線上。對于一個系統來說，進入開發階段后，開發人員每天都要完成一定量的代碼行，而代碼行的總數在項目計劃階段就應當是估算好的，那么，開發人員應當按照怎樣的速度完成這些代碼；已經完成了一部分代碼后，能否判斷出這樣的速度是否合理、能否按期完成任務；前期完成過多代碼可能會造成后期工作量太小，而前期完成太少代碼又可能會帶來后期的工作繁重。也許這時，你就會迫切需要一個工具來對開發人員的工作進行監控。進入測試階段也是一樣。所以這里提到的軟件領域中的成長曲線的預測，就是針對軟件的開發階段和測試階段的。再以測試為例，成長曲線能夠反映缺陷從最初的測試出的缺陷較少，到中期不斷發展增多，再到最終測出的缺陷數穩定不變的全部過程。成長曲線應當是連續的，它能夠表示一段時間內事物持續發展的情況，能夠表示事物在一個持續的時間段內發展的全過程。

　　成長曲線有很多種形式。常見的線性曲線也可以看作是成長曲線的一種，只是在現實中，線性曲線的使用不如非線性曲線廣泛。下面將幾種常見的成長曲線歸納介紹，希望對大家的理解有所幫助。

　　1、Rayleigh模型

　　Rayleigh模型是Weibull分布的一種特殊形式，是一種常用的模型。Weibull分布最重要的一個特征是它的概率密度函數的尾部逐漸逼近0，但永遠達不到0，在許多工程領域都使用了很多年。Rayleigh模型既可以對軟件開發全生命周期進行預測，也可以僅對測試階段的缺陷分布進行預測，得到所期望的時間間隔t與所發現缺陷的關系。對于成熟的組織，當項目周期、軟件規模和缺陷密度已經確定時，就可以得到確定的缺陷分布曲線，并可以據此控制項目過程的缺陷率。如果項目進行中實際的缺陷值與預估的缺陷值有較大差別時，說明中間出現問題，需要加以控制。

　　1）Rayleigh模型的函數形式

　　Rayleigh模型的累積分布函數（CDF）：F（t）=K*（1-exp^（-（t/c）^2））；

　　Rayleigh模型的概率密度函數（PDF）：f（t）=2*K*t/（c^2）*（ exp^（-（t/c）^2））。

　　上面兩個函數中，t是時間自變量，c是一個常量（c=2^（1/2）tm，tm是f（t）到達峰值對應的時間），K是曲線與坐標形成的面積（總缺陷數），也是我們要估計的參數。多年的預測經驗得到缺陷在tm時間的比率（F（tm）/K）約等于0.4，即在f（t）到達最大值時，已出現的缺陷大約占總缺陷的40%。按照這個推導，在某一時間就可以估算出總的缺陷數以及具體的Rayleigh分布參數，從而將缺陷的計算過程簡化。

　　2）Rayleigh函數對應的圖

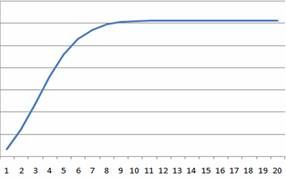
圖1 Rayleigh模型的CDF圖

圖2 Rayleigh模型的PDF圖

　　由圖1——CDF圖可以看出，累積密度最終趨近一個最大值（K）；由圖2——PDF圖可以看出，缺陷隨時間逐漸降低最終趨向于0。

）使用Rayleigh曲線來建模軟件開發質量涉及兩個假設：

　　在開發過程中觀察到的缺陷率與應用中的缺陷率成正比關系。對應于圖1來說，也就是如果開發過程中觀測到的缺陷率越高，CDF中圖的幅度越高，K值越大；

　　給定同樣的錯誤植入率，假如更多的缺陷被發現并更早將其移出，那么在后期階段遺留的缺陷就更少，應用領域的質量就更好。對應于圖2來說，曲線與X、Y軸圍成區域的面積是一定的（總的缺陷數是確定的），如果在前期移除較多缺陷，即曲線的峰值點前移，那么后期曲線的面積就會小，代表后期遺留的缺陷數減少。

　　4）使用場景：收集數據應當越早越好；且需要持續的追蹤缺陷數。

　　5）優勢：隨時間信息的缺陷密度可預測，因此在測試階段使得找到并驗證缺陷的估計成為可能。

　　6）Rayleigh模型沒有考慮到變化調整的機制，所以可能會影響到缺陷的預測。

　　2、指數模型

　　指數模型是針對測試階段，尤其是驗收類測試階段的缺陷分布的模型，其基本原理是在這個階段出現的缺陷（或者失效模式，我們這里討論的是缺陷）是整個產品可靠性的良好指證。它是Weibull系列的另一個特例。指數模型是許多其他可靠性增長模型的基礎。指數模型可分為故障/失效計數模型（fault/failure count model）和失效間隔時間模型（time between failures model）。基本的指數模型的累積缺陷分布函數（CDF）為y=K*a*b^t，修正指數模型在基本指數模型曲線函數上加一個常數因子。

　　1）指數模型的函數形式

　　指數模型的累積缺陷分布函數（CDF）：F（t）=K*（1-exp（-λ*t））；

　　指數模型的缺陷概率密度函數（PDF）：f（t）=K*（λ*exp（-λ*t））。

　　其中，t是時間，K是總缺陷數，λ與K是需要估計的兩個參數。

　　2）指數模型對應的函數圖

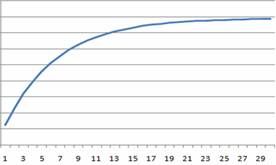
圖3 指數模型的CDF圖

圖4 指數模型的PDF圖

2）指數模型的關鍵假設：測試工作量在測試階段中是均勻的。

　　3）使用：指數模型預測缺陷時是基于正式的測試階段的數據的，因此它主要適用于這些階段，最好在開發過程后期——例如最后的測試階段。但在交付用戶使用后，用戶發現的缺陷模型，與交付用戶之前的模型往往有很大差別，這是由于交付客戶后影響客戶的測試的不確定因素更多。

　　4）優勢：最簡單最有用的模型之一，易于使用和實現。

　　5）缺陷：假設測試的工作量在整個測試階段是均勻的。

　　3、NHPP模型（非齊次泊松過程模型）

　　NHPP模型是對在給定間隔內觀察到的故障數建模，它是指數模型的一個直接應用。

　　1）NHPP模型的函數形式：其中，參數的含義與指數模型相同

　　NHPP模型的累積缺陷分布函數（CDF）：F（t）=K*（1-exp（-λ*t））；

　　NHPP模型的缺陷概率密度函數（PDF）：f（t）=K*λ*c^（-λ*t）。

　　2）NHPP模型對應的函數圖：見指數模型

　　3）由于NHPP模型是指數模型的應用，所以NHPP 模型的特征與指數模型的特征相同。

　　4）缺陷：大多數NHPP模型都基于這樣的假設：每個缺陷的嚴重性和被監測到的可能性相同，在排除一個缺陷時不引入另一個新的缺陷，但實際情況并非如此。缺陷之間是存在著關聯關系的。

　　4、S型可靠性增長模型

　　S型增長模型是軟件領域應用較為廣泛的模型之一，下一篇，將會詳細進行介紹。

　　未完待續。。。