一、正交表的由來
1、拉丁方名稱的由來
古希臘是一個多民族的國家,國王在檢閱臣民時要求每個方隊中每行有一個民族代表,每列也要有一個民族的代表。
數學家在設計方陣時,以每一個拉丁字母表示一個民族,所以設計的方陣稱為拉丁方。
2、什么是n階拉丁方?
用n個不同的拉丁字母排成一個n階方陣(n<26 ),如果每行的n個字母均不相同,每列的n個字母均不相同,則稱這種方陣為n*n拉丁方或n階拉丁方。每個字母在任一行、任一列中只出現一次。
3、什么是正交拉丁方?
設有兩個n階的拉丁方,如果將它們疊合在一起,恰好出現n2個不同的有序數對,則稱為這兩個拉丁方為互相正交的拉丁方,簡稱正交拉丁方。
例如:3階拉丁方
A B C A B C
B C A 和 C A B
C A B B C A
用數字替代拉丁字母:
1 2 3 1 2 3 (1,1)(2,2)(3,3)
2 3 1 和 3 1 2 ---> (2,3)(3,1)(1,2)
3 1 2 2 3 1 (3,2)(1,3)(2,1)
二、正交試驗法介紹
人類在認識自然界的過程中,進行著多方面的探索,試驗是構成學習過程的一個重要要素。
愛迪生一生艱苦奮斗,經歷了無數次的失敗之后,為人類發明了許多重要的科技成果。他的座右銘是:“天才靠的是百分之一的靈感和百分之九十九的汗水”。他的助手在他去世后的第二天說:“如果在愛迪生工作的黑屋中能有一支蠟燭照亮他前進的方向,以他蜜蜂般地努力,他會獲得遠比他發明多的多的成果”。就是說如果有一點理論知識和計算能幫助愛迪生,他會節省90%的精力。愛迪生是邊試驗邊分析后決定下次試驗,這種方法速度太慢。
正交試驗設計是研究多因子(術語解釋:把實驗中影響響應變量的那些變量稱為實驗中的因子,因子分為可控因子和非可控因子)多水平(術語解釋:把因子不同的取值稱為水平)的一種試驗方法,它是根據正交性從全面試驗中挑選出有代表性的點進行試驗,正交試驗具備了“均勻分散,齊整可比”的特點,正交試驗設計是分式析因設計的主要方法。
日本著名的統計學家田口玄一將正交試驗選擇的水平組合列成表格,稱為正交表。例如作一個三因素三水平的實驗,按全面實驗要求,須進行33=27種組合的實驗,且尚未考慮每一組合的重復數。若按L9(33) 正交表安排實驗,只需作9次,大大減少了工作量。正交實驗設計是一種高效率、快速經濟的實驗設計方法,因此在很多領域得到廣泛應用。
利用場景法來設計測試用例時, 作為輸入條件的場景非常龐大,以至于得到的測試用例數目多的驚人,給軟件測試帶來沉重的負擔。如果舍棄一些場景又怕測試設計的覆蓋度達不到,將缺陷遺留給客戶。為了有效地減少測試缺陷遺留,合理地減少測試的工時與費用,從2008年開始公司推行正交試驗設計方法進行測試用例的設計。
三、正交表的構成
1、正交表的構成
行數(Runs):正交表中的行的個數,即試驗的次數,也是我們通過正交實驗法設計的測試用例的個數。
因子數(Factors) :正交表中列的個數,即我們要測試的功能點。
水平數(Levels):任何單個因子能夠取得的值的最大個數。正交表中的包含的值為從0到數“水平數-1”或從1到“水平數” 。即要測試功能點的輸入條件。
2、正交表的形式
L行數(水平數因子數)
如:L8(27)
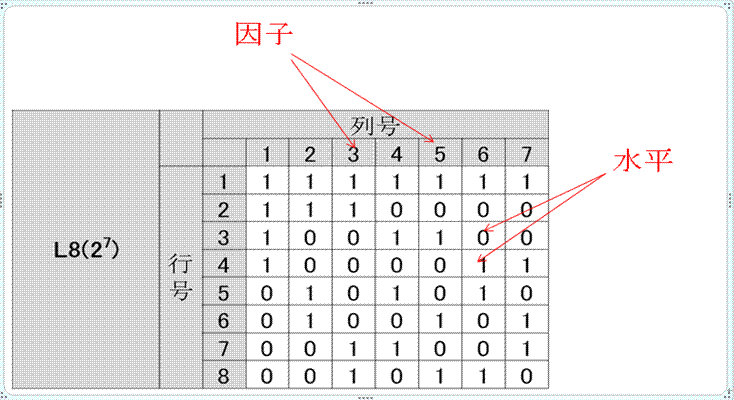
3、正交表的正交性
● 整齊可比性
在同一張正交表中,每個因子的每個水平出現的次數是完全相同的。由于在試驗中每個因子的每個水平與其它因子的每個水平參與試驗的機率是完全相同的,這就保證在各個水平中最大程度的排除了其它因子水平的干擾。因而,能最有效地進行比較,容易找到較佳的試驗條件。
● 均衡分散性
在同一張正交表中,任意兩列(兩個因子)的水平搭配(橫向形成的數字對)是完全相同的。這樣就保證了試驗條件均衡地分散在因子水平的完全組合之中,因而具有很強的代表性,容易得到好的試驗條件。
4、用正交表設計測試用例的優點
● 不需要對所有組合情況窮舉,只需要少量的抽樣組合數據,可明顯地提高效率;
● 用正交表抽樣出的組合數據,對組合情況具有最佳的覆蓋性;
● 能減少手工對組合數據抽樣導致的大量測試遺漏
四、設計步驟
(1)提取功能說明,提取因子
把影響實驗指標的條件稱為因子,而影響實驗因子的條件叫因子的水平。
利用正交實驗設計方法來設計測試用例時,首先要根據被測試軟件的規格說明書找出影響其功能實現的操作對象和外部因素,把它們當作因子;而把各個因子的取值當作狀態,把它們當做水平。對軟件需求規格說明中的功能要求進行劃分,把整體的、概要性的功能要求進行層層分解與展開,分解成具體的有相對獨立性的、基本的功能要求。這樣就可以把被測試軟件中所有的因子都確定下來,并為確定每個因子的權值提供參考的依據。確定因子與狀態是設計測試用例的關鍵。因此要求盡可能全面的、正確的確定取值,以確保測試用例的設計作到完整與有效。
(2)判斷是否可以使用正交表
并不是任何情況都可以使用正交表,以下情況無法使用正交表:
● 因素的個數非常少,如只有2個;
● 因子數很大。
另外在識別的因子中,還要進行以下分析:
● 組合因素之間必須為平行關系(平行:可以同時存在)
● 不能為互斥(互斥:1個因素存在,另1個因素不能存在)
● 因素不能被其它因素的因子制約(制約:當A因素的因子為A1,B因素不能存在)
● 排除非組合因素
(3)查找和調整正交表
如果判斷可以使用正交測試方法設計測試用列,需要根據測試功能點的實際情況,選擇正交表。
選擇正交表的原則如下:
● 實際因素數≤正交表因素數;
● 實際每個因子數≤正交表每個因子數;
● 如果出現2個或2個以上正交表符合以上條件,則選擇Case數最少的正交表。
選取了正交表后,刪除正交表中多余的因子列,原則是刪除靠后的列;
(4)加權篩選,生成因素分析表
對因子與狀態的選擇可按其重要程度分別加權。可根據各個因子及狀態的作用大小、出現頻率的大小以及測試的需要,確定權重的大小。對于權重高的因子放在最前面的列中,以此類推。
(5)把變量的值映射到表中
在使用正交法時,要考慮到被測系統中要準備測試的功能點,而這些功能點就是要獲取的因子,但每個功能點要輸入的數據按等價類劃分有多個,也就是每個因素的輸入條件,即狀態或水平值。
選取了因子和水平后,需要把變量實際的值映射到正交表中。
(6)正交測試用例的制作
把實際因子和水平代入正交表后,每一行制作成一個測試用例。
(7)組合補充測試用例
根據需求規格說明書或錯誤推斷法,補充需要測試但正交表沒有覆蓋的測試數據,將其制作成測試用例。