理論知識終于告一段落啦。接下來要和大家分享的是S型曲線模型中的重要模型——Gompertz模型和Logistic模型在公司內部實際項目中的應用。下面的數據都是來自于公司內部實際項目,應用主要分4個場景:進入測試階段前、測試階段過程中、測試退出時、以及其它的應用。下面將依據場景,從測試階段開始一直到結束,分階段介紹S型曲線的應用。
● 進入測試階段前的缺陷發現目標的預測
進入測試階段前的缺陷預測過程可以說是一個靜態的預估過程。簡單來說,即根據經驗、歷史數據、預測開始時的缺陷數、release時的缺陷數和遺留缺陷數來預測整個測試階段的缺陷趨勢,這個過程通過三點法來完成。最后預測得出的缺陷模型是最初模型,可作為后期階段的指導模型。
● 測試階段每周缺陷發現進度跟蹤與預測
● 測試退出評價時,對無償維護階段發現缺陷數的估計
● 其他
上面介紹的幾種應用場景,都在實際項目中得到了印證。但要想確定推廣模型的使用,首先需要的,就是數據的收集工作。只有數據收集的準確、完整,才有可能得到較為精確的成長曲線模型。
本篇主要介紹第一個場景,即進入測試階段前缺陷發現目標的預測。下面選擇了公司內過程穩定的軟件產品線上的一個升級版本項目作為試點,選擇最常用的S型曲線中的Gompertz和Logistic曲線,在測試階段對缺陷發現趨勢和遺漏進行了估計和跟蹤。實驗過程中使用的工具為公司內部針對軟件缺陷預測開發的基于SRGM的成長曲線預測工具。
1)測試階段準備期對缺陷發現趨勢的估計
進入測試階段前的缺陷預測過程基本是一個靜態的預估過程,即根據軟件規模與經驗、歷史數據、之前開發階段發現的缺陷數等已有數據,版本發布的質量目標(如:單位規模缺陷漏出率)來估計測試階段的缺陷發現趨勢。可通過對進入測試、版本發布判定和版本發布后維護期的三組數據使用三點法來完成。這時估出的缺陷發現趨勢只是初步結果,作為測試階段根據實際數據不斷改進的基礎。
以試點項目為例,根據測試用例實施計劃以及歷史數據,估計出進入測試階段后第一周應發現缺陷25件。根據前一個迭代周期的測試階段缺陷發現率約為12件/KLOC,本次迭代估計代碼規模約為85KLOC;估計出版本發布時(進入測試階段起第14周)應發現缺陷數為1020件。對應版本維護階段(進入測試階段起第27周),根據組織級質量目標,得到遺漏缺陷約68件,合計應發現缺陷數為1088件,由這些數據得到release時的百分比(通過計算得出)。應用三點法,得到如下缺陷發現累積估計值,可作為測試負責人制訂每周發現缺陷目標的重要參考。預測方法如圖1所示。
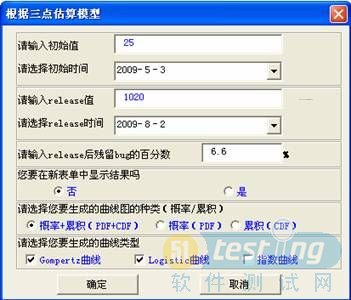
圖1 測試準備階段對缺陷發現趨勢估計
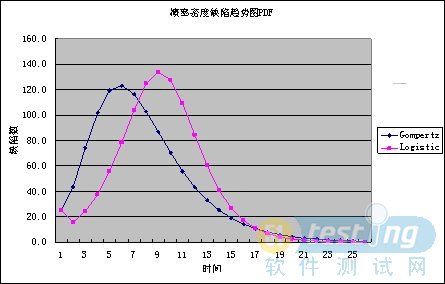
圖2 趨勢預測圖PDF
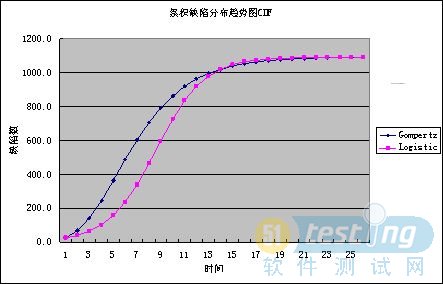
圖3 趨勢預測圖CDF
估計結果如表1數據所示。(看了上面的圖示,相信大家都已經知道百分比的計算方法啦。)
表1 應用三點法得到的缺陷發現累積估計值
所在周 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
原始估計 | 25 | | | | | | | | | | | | | 1020 |
Gompertz | 25 | 68 | 142 | 244 | 363 | 486 | 603 | 706 | 792 | 863 | 919 | 962 | 995 | 1020 |
Logistic | 25 | 40 | 65 | 102 | 157 | 236 | 340 | 464 | 598 | 726 | 835 | 919 | 979 | 1020 |
所在周 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
原始估計 | 1020 | | | | | | | | | | | | | 1088 |
Gompertz | 1020 | 1039 | 1053 | 1063 | 1071 | 1077 | 1081 | 1084 | 1086 | 1088 | 1089 | 1090 | 1091 | 1091 |
Logistic | 1020 | 1047 | 1064 | 1074 | 1081 | 1085 | 1088 | 1089 | 1090 | 1091 | 1091 | 1091 | 1091 | 1091 |
實際項目中,測試負責人根據歷史數據,選擇了Gompertz曲線擬合出的估計值作為每周發現缺陷目標。這樣,就在進入測試階段前,初步確定了測試階段每周應當發現的缺陷目標。當然,這只是一個初始值。
2)測試階段每周對缺陷發現趨勢的進度跟蹤
我們雖然已經利用缺陷預測工具得到了一個每周應當發現缺陷個數的初始值,然而,這個初始值不應當是固定不變的,每周實際發現的缺陷數也可能不會嚴格與預測值一致,可能更多,也可能更少。因此,進入測試階段后,測試負責人跟蹤每周發現的缺陷情況,進行預測值與實際值的對照。在數據量符合算法要求后,使用三和法或高斯-牛頓法(GNL法)模擬、更新缺陷發現趨勢的漸近值K。若有必要,比如測試階段準備期選擇的模型估計值與實際數據發生嚴重偏差時,可能僅更新K值并不能擬合實際的情況,而是需要選擇其它的成長曲線模型。
同樣利用我們的缺陷預測工具。當具有一定的數據量后,即可使用三和法或GNL法重新模擬缺陷趨勢,更新最早發現的缺陷情況。利用同樣的例子,當數據量收集到14個,利用三和法進行預測,分別生成Gompertz曲線和Logistic曲線。下圖4中,選擇要預測的樣本數據;下圖5中,設置預測條件。
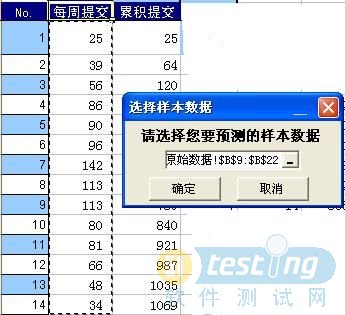
圖4 選擇樣本數據

圖5 缺陷預測參數選擇
選擇預測的數據為27個,得到14周之后的結果如表2。
表2 應用三和法得到的缺陷發現累積估計值
所在周 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
原始估計 | 25 | 64 | 120 | 206 | 296 | 392 | 534 | 647 | 760 | 840 | 921 | 987 | 1035 | 1069 |
Gompertz | 24 | 58 | 116 | 198 | 300 | 413 | 529 | 640 | 743 | 833 | 910 | 974 | 1027 | 1070 |
Logistic | 26 | 47 | 84 | 144 | 237 | 366 | 521 | 676 | 807 | 902 | 964 | 1020 | 1024 | 1036 |
所在周 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
原始估計 | 1069 | 1092 | 1114 | 1139 | 1142 | 1145 | 1158 | 1162 | 1164 | 1165 | 1165 | 1166 | 1166 | 1166 |
Gompertz | 1070 | 1104 | 1131 | 1153 | 1170 | 1183 | 1194 | 1202 | 1208 | 1213 | 1217 | 1220 | 1222 | 1224 |
Logistic | 1036 | 1043 | 1046 | 1049 | 1050 | 1050 | 1051 | 1051 | 1051 | 1051 | 1051 | 1051 | 1051 | 1051 |
從擬合程度可以看出,Gompertz曲線的擬合程度近似100%,而Logistic曲線的擬合程度低于Gompertz曲線,因此,選擇Gompertz曲線作為擬合曲線。
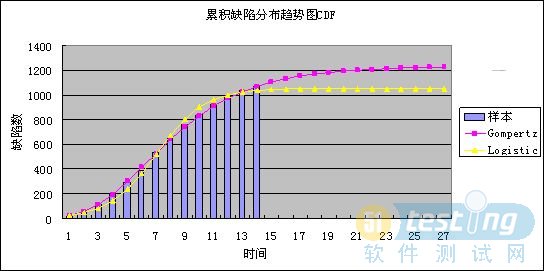
圖6 缺陷趨勢圖CDF
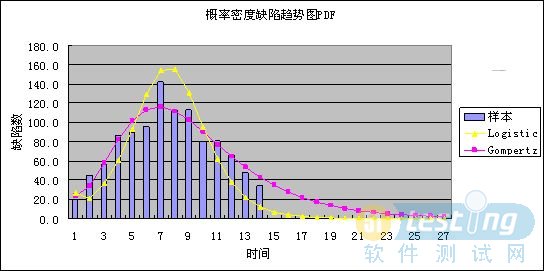
圖7 缺陷趨勢圖PDF
選擇Gompertz曲線得到的K值為1230,即整個系統應當共發現1230個bug。然而如同我們之前關于K值的描述,K值并不是始終都不變的,因此需要在測試階段持續的進行預測,得到更為可靠的結果。
根據預實對照的結果,按照需要調整目前測試的狀態。
-----------------------------------------------------------------------------------------------------------------------
作為一個項目經理或者測試經理,上面提到的內容對你來說應當很容易理解,但你要考慮的恐怕更多。比如,選定要release的時間,根據release時間的安排每周發現缺陷的任務;再比如,公共假期的時間考慮(可能沒有幾個人愿意在春節這樣的假期里繼續工作吧,不過release的時間可是不能修改的)。根據實際情況考慮的更多更全面,才能讓你的預測更加貼近實際,預測的結果才能有效。
3)測試階段結束前的退出標準的評價
準備退出測試階段前,根據預測得到的應發現的缺陷總數、缺陷預測模型和實際發現的缺陷數據,可以模擬版本中仍然遺留的缺陷數,據此可以確定:
● 根據軟件發布標準決定軟件是否能夠如期發布;
● 估計在后續軟件維護階段會發現缺陷的情況,以指導項目確保客戶滿意度的前提下,合理安排人員退出。
以試點項目為例,根據測試階段14周的實際缺陷發現數據,使用三和法,對最常用的Gompertz和Logistic曲線模型,重新實施擬合,結果如表2和圖8所示。
表2 應用三和法重新擬合的缺陷發現累積估計值
所在周 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
原始估計 | 25 | 64 | 120 | 206 | 296 | 392 | 534 | 647 | 760 | 840 | 921 | 987 | 1035 | 1069 |
Gompertz | 24 | 58 | 116 | 198 | 300 | 413 | 529 | 640 | 743 | 833 | 910 | 974 | 1027 | 1070 |
Logistic | 26 | 47 | 84 | 144 | 237 | 366 | 521 | 676 | 807 | 902 | 964 | 1020 | 1024 | 1036 |
所在周 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
原始估計 | 1069 | 1092 | 1114 | 1139 | 1142 | 1145 | 1158 | 1162 | 1164 | 1165 | 1165 | 1166 | 1166 | 1166 |
Gompertz | 1070 | 1104 | 1131 | 1153 | 1170 | 1183 | 1194 | 1202 | 1208 | 1213 | 1217 | 1220 | 1222 | 1224 |
Logistic | 1036 | 1043 | 1046 | 1049 | 1050 | 1050 | 1051 | 1051 | 1051 | 1051 | 1051 | 1051 | 1051 | 1051 |

圖8 試點項目的缺陷預測情況
經過計算,Gompertz曲線的R2值高達99.93%,說明模型對實際數據的擬合程度很高,其漸近值對發布后缺陷趨勢有較高參考價值。根據Gompertz曲線的預估趨勢,發現若第14周結束測試階段,則缺陷遺留率有可能高達14%,無法滿足本項目的質量目標。因此增加了2周時間的回歸測試,使版本發布后的缺陷遺留率最終控制在5%以內。而實際項目中,往往不希望額外的2周測試時間造成版本發布時間推后,這樣可以在版本發布預定時間之前采取一些補救措施。首先,在版本發布之前,就根據模型預估的缺陷圖計算出發布時的缺陷遺留率,若不能滿足發布要求,則即時采取措施,比如,邀請客戶提前參與回歸測試;對測試人員進行培訓;派遣測試人員到客戶處進行業務學習,提高業務能力等等。
4)其他場景
除了測試階段利用S型曲線對缺陷進行預測外,還可以對Gompertz和Logistic曲線模型使用三點法與三和法,來預測與跟蹤測試階段缺陷修改累積趨勢(即每周應當修改多少缺陷,以此來控制缺陷修改的進度)和編碼階段代碼規模增長趨勢(即每周應當完成的代碼工作量,以此來控制編碼開發的資源投入與進度)。在軟件開發不同的生命周期階段中,可靠性增長模型還有更多的實際應用場景,支持對過程的量化管理。
至此,軟件可靠性增長模型之S型曲線的介紹就暫時告一段落了。后續我們還將進行補充,利用實際項目中的數據對趨勢預測模型不斷進行完善。