線性回歸主要用最小二乘法得到直線并進(jìn)行預(yù)測。線性回歸真正復(fù)雜的地方在于檢驗(yàn),這篇博客主要總結(jié)線性回歸的檢驗(yàn)。
這篇文字涉及到的檢驗(yàn)主要包括擬合優(yōu)度檢驗(yàn),標(biāo)準(zhǔn)差檢驗(yàn),整體自變量顯著性檢驗(yàn)-F檢驗(yàn),單個(gè)系數(shù)顯著性檢驗(yàn)-t檢驗(yàn)。
線性回歸有一元線性回歸和多元線性回歸,先說一元的。
擬合優(yōu)度檢驗(yàn):
對樣本回歸直線與樣本觀測值之間擬合程度的檢驗(yàn)。用判定系數(shù)(可決系數(shù))檢驗(yàn),R2
對于
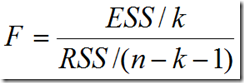
_thumb.png)
_thumb.png)
_thumb.png)
如果Yi=?i 即實(shí)際觀測值落在樣本回歸“線”上,則擬合最好。
可認(rèn)為,“離差”全部來自回歸線,而與“殘差”無關(guān)。
對于所有樣本點(diǎn),則需考慮這些點(diǎn)與樣本均值離差的平方和,可以證明:
_thumb.png)
_thumb.png)
Tss = ESS + RSS
Y的觀測值圍繞其均值的總離差(total variation)可分解為兩部分:一部分來自回歸線(ESS),另一部分則來自隨機(jī)勢力(RSS)。
在給定樣本中,TSS不變,
如果實(shí)際觀測點(diǎn)離樣本回歸線越近,則ESS在TSS中占的比重越大,因此
擬合優(yōu)度:回歸平方和ESS/Y的總離差TSS
_thumb.png)
標(biāo)準(zhǔn)差檢驗(yàn):
估計(jì)標(biāo)準(zhǔn)誤差主要是為了估計(jì)總體方差。
所謂估計(jì)標(biāo)準(zhǔn)誤差是指估計(jì)值與觀察值的平均差異程度, 用( S) 表示。而 S 2是總體方差( σ 2 ) 的無偏估計(jì)量, 即σ^ 2 =S 2 =Σe i的平方 /(n- 2)。該指標(biāo)的意義是: S 越小表明實(shí)際觀測點(diǎn)與所擬和的樣本回歸線的離差程度越小, 即回歸線具有較強(qiáng)的代表性; 反之, S 越大表明實(shí)際觀 測 點(diǎn) 與 所 擬和的樣本回歸線的離差程度越大, 即回歸線的代表性較差。
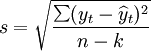
式中:
yt——因變量第t期的觀察值;
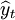 ——因變量第t期的估計(jì)值;
——因變量第t期的估計(jì)值;
n——觀察期的個(gè)數(shù);
k——自由度,為變量的個(gè)數(shù)(包括因變量和自變量)。
判斷回歸標(biāo)準(zhǔn)差能否通過檢驗(yàn),仍用以下公式:式中:
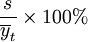
s——回歸標(biāo)準(zhǔn)差;
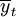 ——因變量觀察值的平均值。
——因變量觀察值的平均值。
當(dāng)依此式計(jì)算出的值小于15%,說明預(yù)測模型通過了回歸標(biāo)準(zhǔn)差檢驗(yàn)。
一元相關(guān)系數(shù)檢驗(yàn):
在回歸分析預(yù)測法中,需要對X、Y之間相關(guān)程度作出判斷,這就要計(jì)算相關(guān)系數(shù)Y,其公式如下:
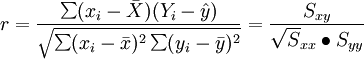
相關(guān)系數(shù)r的特征有:
①相關(guān)系數(shù)取值范圍為:-1≤r≤1 。
②r與b符合相同。當(dāng)r>0,稱正線性相關(guān),Xi上升,Yi呈線性增加。當(dāng)r<0,稱負(fù)線性相關(guān),Xi上升,Yi呈線性減少。
③|r|=0,X與Y無線性相關(guān)關(guān)系;|r|=1,完全確定的線性相關(guān)關(guān)系;0<|r|<1,X與Y存在一定的線性相關(guān)關(guān)系;|r|>0.7,為高度線性相關(guān);0.3<|r|≤0.7,為中度線性相關(guān);|r|≤0.3,為低度線性相關(guān)。
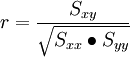
整體自變量顯著性檢驗(yàn)-F檢驗(yàn) & 單個(gè)系數(shù)顯著性檢驗(yàn)-t檢驗(yàn)
這兩種檢驗(yàn)方式在一元中意義是一致的,回歸分析中的假設(shè)檢驗(yàn)包括變量之間的線性關(guān)系檢驗(yàn)和參數(shù)的顯著性檢驗(yàn)兩個(gè)內(nèi)容。前者檢驗(yàn)的是解釋變量 與被解釋變量 能否用一個(gè)線性模型來表示,后者檢驗(yàn)的是回歸模型中的每一個(gè)解釋變量對被解釋變量的影響程度。這兩種檢驗(yàn)在順序上是不能顛倒的。
F檢驗(yàn):
根據(jù)數(shù)從線性回歸模型可以看到,如果變量X和Y之間的線性關(guān)系是顯著的,那么解釋變量X的變化必然引起被解釋變量Y的顯著變化,此時(shí), 一定不為0。否則被解釋變量Y的變化將不依賴于解釋變量X的變化,而僅僅依賴于隨機(jī)誤差項(xiàng)。因此,變量之間線性關(guān)系的檢驗(yàn)問題可以轉(zhuǎn)化為檢驗(yàn)
一定不為0。否則被解釋變量Y的變化將不依賴于解釋變量X的變化,而僅僅依賴于隨機(jī)誤差項(xiàng)。因此,變量之間線性關(guān)系的檢驗(yàn)問題可以轉(zhuǎn)化為檢驗(yàn)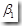 是否為0。由此我們可以給出以下假設(shè):
是否為0。由此我們可以給出以下假設(shè):
原假設(shè) : 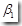 =0 備擇假設(shè) :
=0 備擇假設(shè) : 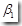 ≠0
≠0
如果原假設(shè)成立,那么統(tǒng)計(jì)量
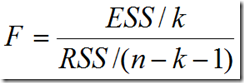
服從自由度為(k , n-k-1)的F分布
如果計(jì)算出的F值大于在給定的顯著性水平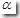 下的臨界值
下的臨界值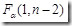 ,則拒絕接受備擇假設(shè),說明解釋變量對被解釋變量有顯著影響,即兩者線性關(guān)系顯著。
,則拒絕接受備擇假設(shè),說明解釋變量對被解釋變量有顯著影響,即兩者線性關(guān)系顯著。
t檢驗(yàn):
構(gòu)造出了一個(gè)比較復(fù)雜的t函數(shù),沒理解,參考中,多元線性回歸分析預(yù)測法和多元線性回歸模型擬合優(yōu)度假設(shè)檢驗(yàn)都寫了具體公式,與F檢驗(yàn)類似,也是t值大于臨界值時(shí),解釋變量有顯著影響。
另外,多元線性回歸分析預(yù)測法也提到了另外兩種預(yù)測,粗略地看了一下:
多重共線性判別
若某個(gè)回歸系數(shù)的t檢驗(yàn)通不過,可能是這個(gè)系數(shù)相對應(yīng)的自變量對因變量的影平不顯著所致,此時(shí),應(yīng)從回歸模型中剔除這個(gè)自變量,重新建立更為簡單的回歸模型或更換自變量。也可能是自變量之間有共線性所致,此時(shí)應(yīng)設(shè)法降低共線性的影響。
當(dāng)回歸模型是根據(jù)動態(tài)數(shù)據(jù)建立的,則誤差項(xiàng)e也是一個(gè)時(shí)間序列,若誤差序列諸項(xiàng)之間相互獨(dú)立,則誤差序列各項(xiàng)之間沒有相關(guān)關(guān)系,若誤差序列之間存在密切的相關(guān)關(guān)系,則建立的回歸模型就不能表述自變量與因變量之間的真實(shí)變動關(guān)系。D.W檢驗(yàn)就是誤差序列的自相關(guān)檢驗(yàn)。檢驗(yàn)的方法與一元線性回歸相同。
參考:
一元線性回歸預(yù)測法:
http://wiki.mbalib.com/wiki/%E4%B8%80%E5%85%83%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92%E9%A2%84%E6%B5%8B%E6%B3%95
[ppt]一元線性回歸模型的統(tǒng)計(jì)檢驗(yàn): http://wenku.baidu.com/view/ca151ff6f61fb7360b4c65d0.html?from=related
二元線性回歸分析預(yù)測法:
http://wiki.mbalib.com/wiki/%E4%BA%8C%E5%85%83%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92%E5%88%86%E6%9E%90%E9%A2%84%E6%B5%8B%E6%B3%95
【doc】第三章 一元線性回歸 http://wenku.baidu.com/view/3b3bdbbdc77da26925c5b0fa.html
多元線性回歸分析預(yù)測法:http://wiki.mbalib.com/wiki/%E5%A4%9A%E5%85%83%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92%E5%88%86%E6%9E%90%E9%A2%84%E6%B5%8B%E6%B3%95