[reference: http://en.wikipedia.org/wiki/Chinese_remainder_theorem & http://en.wikipedia.org/wiki/Extended_Euclidean_algorithm ]

Suppose n₁, n₂, …, n_k are positive integers which are pairwise coprime. Then, for any given integers a₁,a₂, …, a_k, there exists an integer x solving the system of simultaneous congruences

Furthermore, all solutions x to this system are congruent modulo the product N = n₁n₂…n_k.

Hence for all , if and only if .

Sometimes, the simultaneous congruences can be solved even if the n_i's are not pairwise coprime. A solution x exists if and only if:

All solutions x are then congruent modulo the least common multiple of the n_i.

Versions of the Chinese remainder theorem were also known to Brahmagupta (7th century), and appear in Liber Abaci (1202).

[edit] A constructive algorithm to find the solution

This algorithm only treats the situations where the n_i's are coprime. The method of successive substitution can often yield solutions to simultaneous congruences, even when the moduli are not pairwise coprime.

Suppose, as above, that a solution is needed to the system of congruences:

Again, to begin, the product is defined. Then a solution x can be found as follows.

For each i the integers n_i and N / n_i are coprime. Using the extended Euclidean algorithm we can therefore find integers r_i and s_i such that r_in_i + s_iN / n_i = 1. Then, choosing the label e_i = s_iN / n_i, the above expression becomes:

Consider e_i. The above equation guarantees that its remainder, when divided by n_i, must be 1. On the other hand, since it is formed as s_iN / n_i, the presence of N guarantees that it's evenly divisible by any n_j so long as .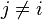

Because of this, combined with the multiplication rules allowed in congruences, one solution to the system of simultaneous congruences is:

For example, consider the problem of finding an integer x such that

Using the extended Euclidean algorithm for 3 and 4×5 = 20, we find (−13) × 3 + 2 × 20 = 1, i.e. e₁ = 40. Using the Euclidean algorithm for 4 and 3×5 = 15, we get (−11) × 4 + 3 × 15 = 1. Hence, e₂ = 45. Finally, using the Euclidean algorithm for 5 and 3×4 = 12, we get 5 × 5 + (−2) × 12 = 1, meaning e₃ = −24. A solution x is therefore 2 × 40 + 3 × 45 + 1 × (−24) = 191. All other solutions are congruent to 191 modulo 60, (3 × 4 × 5 = 60) which means that they are all congruent to 11 modulo 60.

NOTE: There are multiple implementations of the extended Euclidean algorithm which will yield different sets of e₁, e₂, and e₃. These sets however will produce the same solution i.e. 11 modulo 60.

extended Enclidean algorithm

[edit] Informal formulation of the algorithm

Dividend	Divisor	Quotient	Remainder
120	23	5	5
23	5	4	3
5	3	1	2
3	2	1	1
2	1	2	0

It is assumed that the reader is already familiar with .

To illustrate the extension of the Euclid's algorithm, consider the computation of gcd(120, 23), which is shown on the table on the left. Notice that the quotient in each division is recorded as well alongside the remainder.

In this case, the remainder in the fourth line (which is equal to 1) indicates that the gcd is 1; that is, 120 and 23 are coprime (also called relatively prime). For the sake of simplicity, the example chosen is a coprime pair; but the more general case of gcd other than 1 also works similarly.

There are two methods to proceed, both using the division algorithm, which will be discussed separately.

[edit] The iterative method

This method computes expressions of the form r_i = ax_i + by_i for the remainder in each step i of the Euclidean algorithm. Each modulus can be written in terms of the previous two remainders and their whole quotient as follows:

By substitution, this gives:

The first two values are the initial arguments to the algorithm:

r₁ = a = a(1) + b(0)

r₂ = b = a(0) + b(1)

The expression for the last non-zero remainder gives the desired results since this method computes every remainder in terms of a and b, as desired.

Example: Compute the GCD of 120 and 23.

The computation proceeds as follows:

Step	Quotient	Remainder	Substitute	Combine terms
1		120		120 = 120 * 1 + 23 * 0
2		23		23 = 120 * 0 + 23 * 1
3	5	5 = 120 - 23 * 5	5 = (120 * 1 + 23 * 0) - (120 * 0 + 23 * 1) * 5	5 = 120 * 1 + 23 * -5
4	4	3 = 23 - 5 * 4	3 = (120 * 0 + 23 * 1) - (120 * 1 + 23 * -5) * 4	3 = 120 * -4 + 23 * 21
5	1	2 = 5 - 3 * 1	2 = (120 * 1 + 23 * -5) - (120 * -4 + 23 * 21) * 1	2 = 120 * 5 + 23 * -26
6	1	1 = 3 - 2 * 1	1 = (120 * -4 + 23 * 21) - (120 * 5 + 23 * -26) * 1	1 = 120 * -9 + 23 * 47
7	2	0	End of algorithm

The last line reads 1 = −9×120 + 47×23, which is the required solution: x = −9 and y = 47.

This also means that −9 is the multiplicative inverse of 120 modulo 23, and that 47 is the multiplicative inverse of 23 modulo 120.

−9 × 120 ≡ 1 mod 23 and also 47 × 23 ≡ 1 mod 120.

[edit] The recursive method

This method attempts to solve the original equation directly, by reducing the dividend and divisor gradually, from the first line to the last line, which can then be substituted with trivial value and work backward to obtain the solution.

Consider the original equation:

120	x	+	23	y	=	1
(5×23+5)	x	+	23	y	=	1
23	(5x+y)	+	5	x	=	1
...
1	a	+	0	b	=	1

Notice that the equation remains unchanged after decomposing the original dividend in terms of the divisor plus a remainder, and then regrouping terms. If we have a solution to the equation in the second line, then we can work backward to find x and y as required. Although we don't have the solution yet to the second line, notice how the magnitude of the terms decreased (120 and 23 to 23 and 5). Hence, if we keep applying this, eventually we'll reach the last line, which obviously has (1,0) as a trivial solution. Then we can work backward and gradually find out x and y.

Dividend	=	Quotient	x	Divisor	+	Remainder
120	=	5	x	23	+	5
23	=	4	x	5	+	3
...

For the purpose of explaining this method, the full working will not be shown. Instead some of the repeating steps will be described to demonstrate the principle behind this method.

Start by rewriting each line from the first table with division algorithm, focusing on the dividend this time (because we'll be substituting the dividend).

120	x0	+	23	y0	=	1
(5×23+5)	x0	+	23	y0	=	1
23	(5x0+y0)	+	5	x0	=	1
23	x1	+	5	y1	=	1
(4×5+3)	x1	+	5	y1	=	1
5	(4x1+y1)	+	3	x1	=	1
5	x2	+	3	y2	=	1

Assume that we were given x2=2 and y2=-3 already, which is indeed a valid solution. x1=y2=-3 Solve 4x1+y1=x2 by substituting x1=-3, which gives y1=2-4(-3)=14 x0=y1=14 Solve 5x0+y0=x1 by substituting x0=14, so y0=-3-5(14)=-73

[edit] The table method

The table method is probably the simplest method to carry out with a pencil and paper. It is similar to the recursive method, although it does not directly require algebra to use and only requires working in one direction. The main idea is to think of the equation chain as a sequence of divisors . In the running example we have the sequence 120, 23, 5, 3, 2, 1. Any element in this chain can be written as a linear combination of the original x and y, most notably, the last element, gcd(x,y), can be written in this way. The table method involves keeping a table of each divisor, written as a linear combination. The algorithm starts with the table as follows:

a	b	d
1	0	120
0	1	23

The elements in the d column of the table will be the divisors in the sequence. Each d_i can be represented as the linear combination . The a and b values are obvious for the first two rows of the table, which represent x and y themselves. To compute d_i for any i > 2, notice that . Suppose . Then it must be that and . This is easy to verify algebraically with a simple substitution.

Actually carrying out the table method though is simpler than the above equations would indicate. To find the third row of the table in the example, just notice that 120 divided by 23 goes 5 times plus a remainder. This gives us k, the multiplying factor for this row. Now, each value in the table is the value two rows above it, minus k times the value immediately above it. This correctly leads to , , and . After repeating this method to find each line of the table (note that the remainder written in the table and the multiplying factor are two different numbers!), the final values for a and b will solve :

a	b	d
1	0	120
0	1	23
1	-5	5
-4	21	3
5	-26	2
-9	47	1

This method is simple, requiring only the repeated application of one rule, and leaves the answer in the final row of the table with no backtracking. Note also that if you end up with a negative number as the answer for the factor of, in this case b, you will then need to add the modulus in order to make it work as a modular inverse (instead of just taking the absolute value of b). I.e. if it returns a negative number, don't just flip the sign, but add in the other number to make it work. Otherwise it will give you the modular inverse yielding negative one.