這是一個很有用的 公式比如:用戶消費分值權重 , 產品關聯分值權重 等等
公式
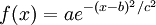
在 http://www.wolframalpha.com 中表示 :
e = (1+1/n) ^n
a*e^(-(x-b)^2/c^2)
a 峰值最大值
b 峰值x軸偏移量
c 弧度跨度
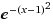
= 1*e^(-(x-1)^2/1^2)
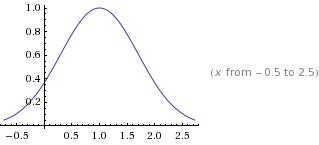
修改 峰值 a = 2
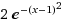
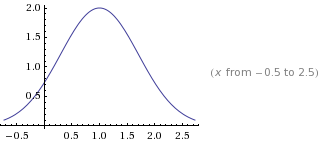
這里 就 不一一展現 b 峰值x軸偏移量 , c 弧度跨度 了 大家可以 去 wolframalpha 自己去嘗試
實例1 與時間有關的遞減 :
import math
def gaussian(x,peak=1.0,axis=1.0,span=1.0):
return peak*math.e**(-(x-axis)**2/(span)**2 )
跨度 c 參考:
c = 1 : 在2.5 附件急劇衰減
c = 2 : 4
c = 18 :30 # 這個數 衰減統計 一個月 不錯
c = 55 :90 # 衰減統計 一個季度 不錯
#簡單應用
消費1次得峰值4分 瀏覽1次峰值2分
統計某用戶季度得分
數據:在前10天瀏覽10次,消費1次 ,前11天瀏覽5次
d10 = gaussian(10,span=55.0)
d11 = gaussian(11,span=55.0)
print d10*10*2+d10*4*1+d11*5*2
#結果 33.0407089687
倒的高斯 - 實例2 :
公式 =


目的 與次數有關的產品分值化
#用戶 對 某產品 分值化
# 比如 某用戶 用過某產品 n次,我希望 n 無限大是一個 漸進某個值 而不是和 n 無限遞增的
#下面的 fun 結果是 1.6 ~ 10 分值直接的區域, 也就是 傳說中的 產品感興趣 “10分制” 簡易版
def gs(x,peak=9.0,axis=-2.0,span=11.0):
return "%.4f" % (-1*peak*math.e**(-(x-axis)**2/(span)**2 )+peak+1)
>>> gs(1)
'1.6451'
>>> gs(2)
'2.1148'
>>> gs(3)
'2.6800'
>>> gs(4)
'3.3161'
>>> gs(5)
'3.9970'
>>> gs(6)
'4.6969'
>>> gs(60)
'10.0000'
整理 m.tkk7.com/Good-Game