canonical

   現代數學是建立在等價類這一概念的基礎之上的。同構是對等價關系的一種刻劃。簡單的可以把它理解為兩個系統之間的一種“保持”運算規則的一一對應關系。在 數學中一個符號所代表的是所有能夠互相同構的對象。例如整數3可以看作是與某個元素個數為3的集合可以建立一一對應關系的所有的集合所構成的整體。所以在 數學中，如果我們解決某個特定的問題，它同時也就意味著我們解決了一系列相互等價的問題。
    同構關系對于認知可以起到本質上的簡化作用。如果通過一個推理鏈條，確認了A == B == C == D，則可以直接從概念上推導出 A == D, 這一關系有可能被直觀理解，而不需要理會中間的推理步驟。（注意到以上元素兩兩建立同構關系的時候可能要采用不同的對應手段，因此上面的等式并不是平凡 的。）另一方面，我們可以確定一個模型元素M,  將系統簡化為 A == M, B == M, C == M, D == M。只要理解了元素M就理解了等價的其他元素。

    Witrix平臺中PDM定義作為基礎的結構模型，它同時映射成為數據庫表，以及hbm, java, meta等多個代碼文件，此外還對應于約定的WebObject名稱和BizFlow文件名稱，相應的報表文件目錄等。我們只要理解了pdm模型，即可通 過推理自然的掌握各個層面上對應的結構。這意味著只要知道實體名稱，就知道如何通過Web訪問這個對象，知道數據在數據庫中對應的數據庫表，而不需要知道 后臺是如何讀取前臺提交的參數以及如何執行保存數據指令的。不僅僅是在模型驅動領域，在系統設計的各個方面，我們都應該盡量充分的利用當前的信息通過推理 得到系統其他部分的結構，而不是通過手工關聯或者判斷在程序中動態維持這種對應關系。例如在flow-cp機制中，biz的id, action的id等都根據step配置的id推導得到，這樣在工作列表跳轉的時候就可以根據規則推導出跳轉頁面對應的鏈接，而不需要手工編寫頁面重定向 代碼。

 
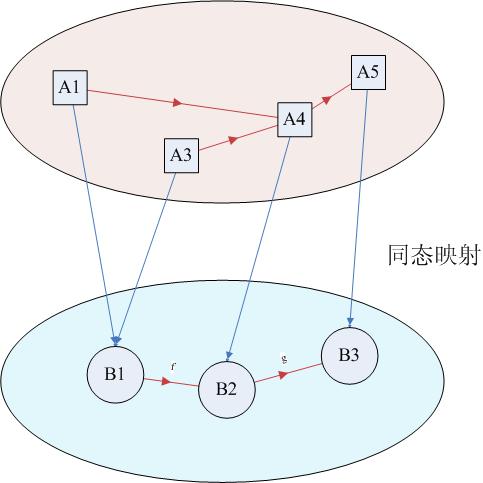
    同態（homomorphism）關系相對于同構關系，只強調單向映射的可行性，它是一個舍棄屬性的過程。同態作為最基礎的認知手段之一，它不僅僅是用一 個符號來置換一組元素，而是同時保留了某種全局的運算關系，因此同態映像可以構成某種獨立的完整的研究對象。通過同態映射，我們可以在不同的抽象層面上研 究原系統的一個簡化版本。例如meta中的layout是一種典型的領域特定語言(DSL)。
    userName userTitle
    emailAddress

每一個字段表示了一個可能任意復雜的inputor或者viewer, 字段之間的前后關系描述了最終顯示頁面上顯示內容的相對關系。當viewer根據需求發生改變的時候，并不影響到layout層面上的關系，因此 layout可以保持不變。如果我們在系統中把問題分解為多個抽象層面上，多個觀察視角上的同態模型，則可能實現更高的軟件復用程度。
    在Witrix平臺的設計中，很多細粒度的標簽都定義為tpl文本段，這樣平臺只要理解某一層面上的交互關系，實際應用中可能出現的細節在標簽內部進行局 部處理，不會突破原始設計的形式邊界，不會影響到原先設定的主體系統結構。例如BizFlow中的tpls段，action的source段等。
    上世紀50年代以前，生物學家做夢也想象不到具有無限復雜性的生物遺傳過程，竟然可以被抽象為ATGC四個抽象符號的串聯。生命竟然不理會各種已知的或是 未知的物理化學作用，被抽象的三聯碼所驅動。一種抽象的本質似乎成了生命世界的本原。在軟件的世界中，可以被識別的抽象元素絕不只是語言本身所提供的那些 機制。