1. 測度定義
“數學上,測度(Measure)是一個函數�����,它對一個給定集合的某些子集指定一個數����,這個數可以比作大小��、體積��、概率等等�����。傳統的積分是在區間上進行的,后來人們希望把積分推廣到任意的集合上����,就發展出測度的概念,它在數學分析和概率論有重要的地位” ——wikipedia
聚類之前一定要定義好向量之間的相似程度——即近鄰測度����。在聚類過程中我們使用的測度,范圍要更廣泛��,首先定義向量之間的測度,接著就是集合與向量��,集合之間的測度。
對于X上的不相似測度(Dissimilarity Measure, DM) d 是一個函數: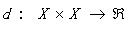 其中R是實數集合,如果d有以下的屬性:
其中R是實數集合,如果d有以下的屬性:
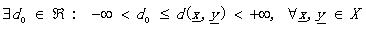 (1.1)
(1.1)
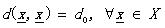 (1.2)
(1.2)
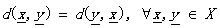 (1.3)
(1.3)
如果又滿足
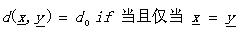 (1.4)
(1.4)
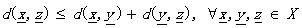 (1.5)
(1.5)
那么d被稱為度量DM����。其中的公式(1.5)也叫三角不等式��。稍稍解釋一下(其實太好理解了)����,不相似性測度其實就像我們說的距離一樣��,兩個向量代表兩個對象好了�����。公式1.2定義(向量)對象自己和自己的距離是d0����;公式1.1說明了任意兩個對象之間的距離要小于正無窮卻大于自己和自己的距離(你和別人的距離大于你和自己的距離,這不廢話嗎^_^);公式1.3說明距離的交互性;公式1.4不解釋了�����,公式1.5就是三角不等式(初中水平)�����。
同理相似性測度(Similarity Measure, SM)定義為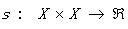 滿足:
滿足:
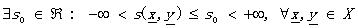 (1.6)
(1.6)
 (1.7)
(1.7)
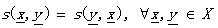 (1.8)
(1.8)
如果又滿足
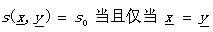 (1.9)
(1.9)
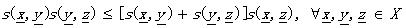 (1.10)
(1.10)
就把s叫做度量SM��。具體同DM,各公式的表達一目了然哦~~~
從定義和字面上我們都可以看出二者的不同,在表達相似性時兩者都可以����,只不過度量的角度不同,對于判別相似,DM越大說明越不相似�����,越小則越相似����,而SM卻正好相反,因此我們也可以聯想,DM與SM可以利用這種對立關系來定義����。舉例來說����,如果d是一個DM,那么s=1/d就是一個SM。
2. 向量之間的近鄰測度
上面的定義只是一個宏觀的概括��,那么具體的向量之間的測度如何計算呢?下面將詳細的介紹�����。
首先對于實向量的不相似測度����,實際應用中最通用的就是加權lp度量了:
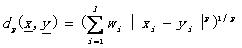 (2.1)
(2.1)
其中的xi和yi分別是向量x和y中的第i個值,wi是第i個權重系數�����,l是向量的維數(以下公式定義同)�����。而我們比較感興趣的就是當p=1時�����,該度量就是加權Manhattan范數����,而當p=2時就是加權歐幾里得范數��,當p=∞時就是max1£i£l wi|xi-yi|了����。根據這些DM��,我們定義SM為bmax - dp(x,y)��。
另外還有一些其他的定義方法,比如
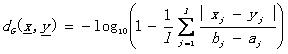 (2.2)
(2.2)
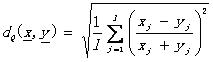 (2.3)
(2.3)
其他懶得列出了��,先查閱資料����,這里不詳述了。
對于實向量的相似性測度����,實際中常用的有:
內積: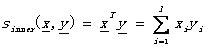 (2.4)
(2.4)
Tanimoto測度: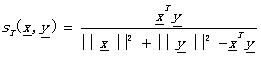 (2.5)
(2.5)
其他: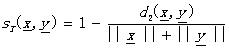 (2.6)
(2.6)
------------------------------------------------take a nap------------------------------------------------------------
對于離散值的向量����,首先必須要搞清楚一個概念,這里在《模式識別》的中文譯作中我感覺翻譯的并不好理解��,所以這里展開說明一下�����,那就是一個叫做相依表(contingency table)的概念�����。對于一個向量x��,其元素值屬于有限集F={0,1,…,k-1}����,其中k是正整數��。令A(x,y)=[aij], i, j=0,1,…,k-1是一個k階方陣��,其中元素aij代表在x中所有i值所在的位置在y的同樣位置有j值的個數�����。附原文:the number of places where x has the i-th symbol and y has the j-th symbol����。舉例來說吧�����,k=3,且x=[0,1,2,1,2,1]�����,y=[1,0,2,1,0,1],那么A(x,y) = [0 1 0, 1 2 0, 1 0 1]�����。以第一個0(a00)為例說明��,0在A中的位置決定i=0����,j=0��,在x中0所在的位置是第一個位置��,而y中0所在的位置為第二個和第五個����,兩個向量中沒有相同位置上的相同0元素�����,因此A中第一個元素a00為0,而A中第二個為1(a01)����,所以i=0�����,j=1����,在x中0所在的位置是第一個��,而y中1所在的位置為第一�����、四、六個��,因此有一個相同�����,所以a01=1�����。
關于計算矩陣A這里附加java代碼實現,可參考:
1
 /** *//**
/** *//**
2 *
*
3 * @param k
* @param k
4 * the number of finite set F
* the number of finite set F
5 * @param x
* @param x
6 * the vector x belongs to F^l
* the vector x belongs to F^l
7 * @param y
* @param y
8 * the vector y belongs to F^l
* the vector y belongs to F^l
9 * @return the contingency table A
* @return the contingency table A
10 * @author $Jia Yu
* @author $Jia Yu
11 */
*/
12 public Integer[][] calContingencyTable(Integer k, Vector<Integer> x,
public Integer[][] calContingencyTable(Integer k, Vector<Integer> x,
13
 Vector<Integer> y)
Vector<Integer> y)  {
{
14 if (x.size() != y.size())
if (x.size() != y.size())
15 throw new IllegalArgumentException(
throw new IllegalArgumentException(
16 "The two vectors are not the same size!");
"The two vectors are not the same size!");
17 Integer[][] A = new Integer[k][k];
Integer[][] A = new Integer[k][k];
18 Integer count_ij;
Integer count_ij;
19
 for (int i = 0; i < k; i++)
for (int i = 0; i < k; i++)  {
{
20
 for (int j = 0; j < k; j++)
for (int j = 0; j < k; j++)  {
{
21 count_ij = 0;
count_ij = 0;
22
 for (int xi = 0; xi < x.size(); xi++)
for (int xi = 0; xi < x.size(); xi++)  {
{
23 if (x.elementAt(xi).equals(i) && y.elementAt(xi).equals(j))
if (x.elementAt(xi).equals(i) && y.elementAt(xi).equals(j))
24 count_ij++;
count_ij++;
25 }
}
26 A[i][j] = count_ij;
A[i][j] = count_ij;
27 }
}
28 }
}
29 return A;
return A;
30 }
}
有了相依表的定義�����,可以定義離散向量之間的不相似性測度了�����。
漢明距離: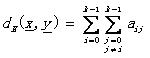 (2.7)
(2.7)
L1距離: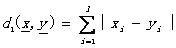 (2.8)
(2.8)
同樣�����,相似性測度有
Tanimoto測度: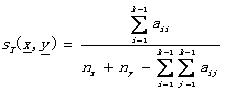 (2.9)
(2.9)
其中的nx( ny)表示x(y)中非零元素的個數��。
書本往往教給我們的是基礎而不是應用,這些基礎知識在實際應用中才會得到更多的改進和變化�����。也許我們不會簡單的在聚類中應用這些測度概念��,但是復雜的組合都是來源于基礎��。因此��,對測度的基礎概念一定要牢牢把握����。在前一階段做圖像分割時,聚類算法執行的前提之一測度,我就做過多個實驗����,L1和L2范數,Tanimoto測度等。當然不同的圖像特征有不同的計算距離方法,總之實際的經驗告訴我,基礎扎實后�����,在應用起來是相當的順手啊~~~(最起碼不會被復雜公式嚇到)
3. 特殊情況處理
考慮到實例向量的特征類型往往是復雜混合的����,這種情況下����,如何計算近鄰測度呢?一些偷懶的做法就是將所有值都看作是實值類型�����,把混合向量當作實向量來處理����。但是現實使用中����,這樣做的效果往往差強人意����?����?紤]將實值類型轉換成離散類型��,這就是著名的離散化了����,特征的離散化操作時特征或屬性過濾(filter)的一個重要的方面��。當然我最推薦的還是基于自己開發的應用場景����,設計相關的近鄰測度�����。這樣可能通用性比較差,但是如果是問題驅動的話����,或者目標驅動��,那么這個作為一個solution也不失優良性。當然引入模糊測度的概念也是一種解決方法����,這里就不細說了�����,具體應用可以參看有關模糊和不確定性的文章��。另外一點需要說明就是實例向量中部分特征丟失的情況�����,對于丟失數據�����,如果我們知道數據的分布,那么合理假設是一個替代方案,但是如果為了省事,常用的做法是直接丟棄該實例向量,或者好點的做法是取所有實例的平均數據作為該維度的替代數據����。
4. 點與集合之間的測度
隨著聚類過程的不斷進行��,層次逐漸深入�����,聚類已經不僅僅是判斷點與點之間的相似程度了����,點與集合的相似程度也需要計算。而如何定義向量x和聚類C之間的近鄰性��,從而判斷是否將x歸類為C�����。以下三個定義經常用到��。
最大近鄰函數Max proximity function: 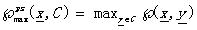 (4.1)
(4.1)
最小近鄰函數Min proximity function: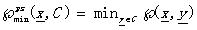 (4.2)
(4.2)
平均近鄰函數Average proximity function: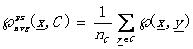 (4.3)
(4.3)
其中nc是集合C的勢。
可以看到��,這樣的定義在概念理論層次上仍舊將點視作點,將聚類視作集合��。另一種情況則是將聚類視作一個點�����,因為點與點之間的近鄰測度已經可以計算�����,那么將集合視為一個點����,就將這個問題歸約到了點與點之間的問題了����。對聚類進行表達��,主要有以下幾種表達:
1) 點表達:將聚類視作一個點����,可以是均值點(mean vector),也可以是均值中心(mean center)�����,也可以是中值中心(median center)��。關于這幾個概念和公式,任何的統計教材里都有涉獵��,我就不一一枚舉了����。(主要貼公式真的很累����,懷念Tex)
2) 超平面表達:線性聚類中常用����。不表。有興趣者去查資料。
3) 超球面表達:球形聚類中常用。同上�����。
一切的學習都為應用����,根據實際應用的不同,我們在定義這種點與集合之間測度時候也有很大的靈活性。
5. 集合與集合之間的測度
同樣的����,對于集合與集合的測度,可以同點與集合的測度類似��。只要記住一點�����,那就是集合與集合間的近鄰測度是建立在點與點之間的測度的基礎上的��。所以近鄰測度的基礎在點與點之間��。當然聚類結果的優化是一個反復試驗的過程,其中也要考慮領域專家的意見�����。
6. 小結
對于近鄰測度的學習����,乍一看像是純數學知識的學習,其實則是對我們開始聚類算法研究之前的一個夯實基礎的復習過程。
7. 參考文獻及推薦閱讀
[1]Pattern Recognition Third Edition, Sergios Theodoridis, Konstantinos Koutroumbas
[2] http://zh.wikipedia.org/wiki/%E6%B5%8B%E5%BA%A6%E8%AE%BA
[3]模式識別第三版, Sergios Theodoridis, Konstantinos Koutroumbas著, 李晶皎, 王愛俠, 張廣源等譯