負數沒有直接的幾何意義��,因此它被認為是對應于不存在的事物。而按照古希臘的邏輯��,不存在的事物是不可能存在的��,因而也就是無法被理解的��,更不可能參與到
推理過程中,因此是無意義的��,無法被定義的��,
因此它是不存在的��。中國人注重的是運算的合理性,而不是數的真理性,大概在公元前400年左右就創造了負數和零的概念��。而在西方直到公元7世紀(唐代)的
一本印度人的著作中才出現負數��,它被用來表示負債��。西方人沒有能夠創造負數,他們對負數的接受更遲至15世紀左右。這件事實在一定程度上說明了存在某種深
刻的困難阻礙我們理解負數概念��。
在引入負數之前��,3x^2 + 8 = 4x 和 3x^2 + 4x + 8 = 0
這兩個方程的結構是完全不同的��,它們需要不同的求解技術,因此也就不可能利用符號抽象出 a x^2 + b x + c =
0��。引入負數才使得我們能夠以統一的方式提出問題��,并研究通用的求解技術。
群論(Group Theory)是對結構進行抽象研究的數學分支��。群的定義包括四條規則
1. 元素之間的運算滿足結合律 (a * b) * c = a * (b * c)
2. 元素之間的運算封閉��,即 a * b 仍然屬于該群
3. 存在單位元��,即對所有a, a * e = e*a = a
4. 每個元素存在對應的逆元,a * a^-1= e
逆運算是非常重要的結構要求��,逆元是對負數的一種抽象推廣��。如果沒有逆元��,則只能構成半群(semi-group),它的性質要少很多��。
目前軟件設計中所有的原則都指向組裝過程��,從無到有��,層層累進。構件組裝的隱喻中所包含的圖像是操縱實際可見的積木��,是缺少逆元概念的��。
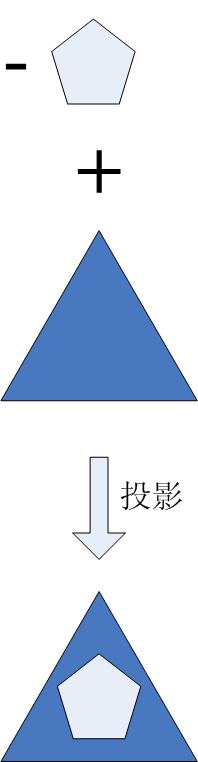
考察一個簡單的例子��,假設需要的產品是三角形內部挖去一個五邊形的剩余部分。有三種生產策略:
1. 對最終需要的產品形態進行三角剖分��,使用8個小三角形拼接出來��。這種方式比較繁瑣��,而且最后粘接工序的可靠性和精確性值得懷疑。
2. 拿到一個真實的三角形��,然后用刀在內部挖出一個五邊形的洞��。這種方式需要消耗一定的人工��,而且也很難保證五邊形的精確性,即使我們曾經精確的生產過其他五角形和三角形��。實際上一般情況下我們是逐步銼出一個五邊形的��,并沒有充分利用到五邊形的對稱性。
3. 在概念空間中做一個抽象計算 (-五邊形) + (三角形) = 所需產品
如果我們能夠生產一種負的五邊形和一種正的三角形,則可以立刻得到最終的產品��。
在軟件開發的實踐中��,我們目前多數采用的是兩種方式:
1. 采用可視化設計工具通過拖拽操作開發出完整的界面和后臺
2. 拷貝一些已有的代碼��,刪除掉不需要的部分,增加一些新的實現,也可能對已有實現做一些不兼容的修正��。
在第二種方式中
新結構的構造 = 已有結構 + 軟件之外的由人執行的一個剪裁過程
這個剪裁過程表現為一個時間序列��。如果我們對原有結構進行了調整��,則需要重新關聯一個時間序列,而此時間序列并不會自動重播��。為了壓縮以時間為度量單位的
生產成本��,我們必須減少對時間序列的依賴��。在時間序列中展開的一個構造過程可以被轉化為一個高維設計空間中的一種更加豐富的構造原理��,我們最終的觀測可以
看作是設計空間向物理空間的一個投影(想象一束光打下來)。這種方式更容易保證程序的正確性��。
時間序列 --[原理轉化]--> 空間關系
這樣我們就可以使用第三種生產策略:利用構造原理進行抽象計算��。如果我們只盯著產品的最終形態看��,只是想著怎么把它像搭積木一樣搭建出來,就不可能識別出
系統結構本身所蘊含的對稱性��。如果我們發現了系統內蘊的結構特征��,但是卻只能通過構造過程中的行動序列來追隨它��,同樣無法實現有效的工作復用。同時因為這
個行動序列一般處于系統規則約束之外��,完全由人的自覺來保障��,因此很難保證它的正確性?�,F實世界的規范要求并不是模型本身所必須滿足的��,只要我們能夠創造
新的結構原理��,在概念空間中我們就可以擁有更多的自由。現在業內鼓吹的軟件構造原理多半是參照物理世界中生產具體物質產品的生產工序��,卻沒有真正把握信息的抽象本質��。掌握規則��,制訂規則,才是信息空間中的游戲規則。
物理學中最重要的分析學思想之一是微擾論(Perturbation).
針對一個復雜的物理現象��,首先建立一個全局的規范的模型��,然后考慮各種微擾條件對原有模型的影響��。在小擾動情況下,模型的變化部分往往可以被線性化,被局
域化��,因而問題得到簡化��。微擾分析得到的解依賴于全局模型的解而存在��,因而這是一種主從關系的分解方式。但是如果主體模型是我們已經熟知的物理現象,則我
們關注的重點可以全部放在擾動解上��,認為所有特定的物理規律都體現在擾動解中��。如果微擾分析得到的物理元素足夠豐富��,則微擾模型本身可以成為獨立的研究對
象,在其中我們同樣可以發現某種普適的結構規律。
考察如下的構造過程
X = a + b + c
Y = a + b + d = (a + b + c) - c + d = X - c + d
對于數學而言��,上述的推導是等價的��,但是對于物理學而言��,Y = a + b + d 和 Y = X - c +
d是有著本質不同的。第一種方式要求打破原先X的構造��,而重新的組裝其實是有成本的��,特別是在X本身非常復雜的情況下。典型的��,如果X是經過測試的功能��,
重新組裝后原先由測試保障的概念邊界被打破��。
我們可以從Y = X + dX抽象出擾動模型 dX = - c + d
主從分解模式自然的導出逆元概念。
如果沒有逆元��,我們必然需要分解��。但是如果發掘了背景這一概念��,在逆元運算下,對背景不是分解讓其成為可見的部分��,而是采用追加的��,增刪的方法對背景結構
進行修正��,則我們有可能在沒有完整背景知識的情況下,獨立的理解局部變化的結構��。即背景是透明的��,知識成為局部的��。在Witrix平臺中,BizFlow
+ DaoWebAction + StdPage
才構成完整的程序模型��,BizFlow其實是對標準模型的差異描述,但是它可以被單獨的理解��。如果我們從接觸程序開始就接受BizFlow,
就可能完全不需要了解數據庫訪問和前臺界面渲染的知識��。我們并不是通過在DaoWebAction中設定各種可預見的調用形式��,而是在BizFlow中通
過類似AOP的操作方式直接對標準模型進行修正。這種修正中一個很重要的部分就是刪除標準模型中缺省提供的功能��。
WebMVC之前世今生 http://canonical.javaeye.com/blog/163196
Witrix架構分析 http://canonical.javaeye.com/blog/126467
變化的部分構成獨立于原始模型的新的模型��,它的結構關系是完備的��,可以獨立的理解。在原始模型崩潰的情況下��,它仍然可能保持有效性��。
從物理學的角度看,我們所觀測到的一切物理現象��,都是某種物理作用的結果��,也就是物質結構相對于背景狀況的一種偏離��。我們只可能觀測到變化的部分,因此我們對世界的認識其實只是世界的擾動模型而已��,世界的本體不屬于科學研究的范疇��。