負(fù)數(shù)沒(méi)有直接的幾何意義,因此它被認(rèn)為是對(duì)應(yīng)于不存在的事物。而按照古希臘的邏輯,不存在的事物是不可能存在的,因而也就是無(wú)法被理解的,更不可能參與到
推理過(guò)程中,因此是無(wú)意義的,無(wú)法被定義的,
因此它是不存在的。中國(guó)人注重的是運(yùn)算的合理性,而不是數(shù)的真理性,大概在公元前400年左右就創(chuàng)造了負(fù)數(shù)和零的概念。而在西方直到公元7世紀(jì)(唐代)的
一本印度人的著作中才出現(xiàn)負(fù)數(shù),它被用來(lái)表示負(fù)債。西方人沒(méi)有能夠創(chuàng)造負(fù)數(shù),他們對(duì)負(fù)數(shù)的接受更遲至15世紀(jì)左右。這件事實(shí)在一定程度上說(shuō)明了存在某種深
刻的困難阻礙我們理解負(fù)數(shù)概念。
在引入負(fù)數(shù)之前,3x^2 + 8 = 4x 和 3x^2 + 4x + 8 = 0
這兩個(gè)方程的結(jié)構(gòu)是完全不同的,它們需要不同的求解技術(shù),因此也就不可能利用符號(hào)抽象出 a x^2 + b x + c =
0。引入負(fù)數(shù)才使得我們能夠以統(tǒng)一的方式提出問(wèn)題,并研究通用的求解技術(shù)。
群論(Group Theory)是對(duì)結(jié)構(gòu)進(jìn)行抽象研究的數(shù)學(xué)分支。群的定義包括四條規(guī)則
1. 元素之間的運(yùn)算滿足結(jié)合律 (a * b) * c = a * (b * c)
2. 元素之間的運(yùn)算封閉,即 a * b 仍然屬于該群
3. 存在單位元,即對(duì)所有a, a * e = e*a = a
4. 每個(gè)元素存在對(duì)應(yīng)的逆元,a * a^-1= e
逆運(yùn)算是非常重要的結(jié)構(gòu)要求,逆元是對(duì)負(fù)數(shù)的一種抽象推廣。如果沒(méi)有逆元,則只能構(gòu)成半群(semi-group),它的性質(zhì)要少很多。
目前軟件設(shè)計(jì)中所有的原則都指向組裝過(guò)程,從無(wú)到有,層層累進(jìn)。構(gòu)件組裝的隱喻中所包含的圖像是操縱實(shí)際可見的積木,是缺少逆元概念的。
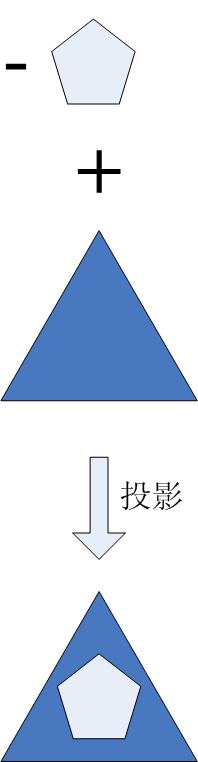
考察一個(gè)簡(jiǎn)單的例子,假設(shè)需要的產(chǎn)品是三角形內(nèi)部挖去一個(gè)五邊形的剩余部分。有三種生產(chǎn)策略:
1. 對(duì)最終需要的產(chǎn)品形態(tài)進(jìn)行三角剖分,使用8個(gè)小三角形拼接出來(lái)。這種方式比較繁瑣,而且最后粘接工序的可靠性和精確性值得懷疑。
2. 拿到一個(gè)真實(shí)的三角形,然后用刀在內(nèi)部挖出一個(gè)五邊形的洞。這種方式需要消耗一定的人工,而且也很難保證五邊形的精確性,即使我們?cè)?jīng)精確的生產(chǎn)過(guò)其他五角形和三角形。實(shí)際上一般情況下我們是逐步銼出一個(gè)五邊形的,并沒(méi)有充分利用到五邊形的對(duì)稱性。
3. 在概念空間中做一個(gè)抽象計(jì)算 (-五邊形) + (三角形) = 所需產(chǎn)品
如果我們能夠生產(chǎn)一種負(fù)的五邊形和一種正的三角形,則可以立刻得到最終的產(chǎn)品。
在軟件開發(fā)的實(shí)踐中,我們目前多數(shù)采用的是兩種方式:
1. 采用可視化設(shè)計(jì)工具通過(guò)拖拽操作開發(fā)出完整的界面和后臺(tái)
2. 拷貝一些已有的代碼,刪除掉不需要的部分,增加一些新的實(shí)現(xiàn),也可能對(duì)已有實(shí)現(xiàn)做一些不兼容的修正。
在第二種方式中
新結(jié)構(gòu)的構(gòu)造 = 已有結(jié)構(gòu) + 軟件之外的由人執(zhí)行的一個(gè)剪裁過(guò)程
這個(gè)剪裁過(guò)程表現(xiàn)為一個(gè)時(shí)間序列。如果我們對(duì)原有結(jié)構(gòu)進(jìn)行了調(diào)整,則需要重新關(guān)聯(lián)一個(gè)時(shí)間序列,而此時(shí)間序列并不會(huì)自動(dòng)重播。為了壓縮以時(shí)間為度量單位的
生產(chǎn)成本,我們必須減少對(duì)時(shí)間序列的依賴。在時(shí)間序列中展開的一個(gè)構(gòu)造過(guò)程可以被轉(zhuǎn)化為一個(gè)高維設(shè)計(jì)空間中的一種更加豐富的構(gòu)造原理,我們最終的觀測(cè)可以
看作是設(shè)計(jì)空間向物理空間的一個(gè)投影(想象一束光打下來(lái))。這種方式更容易保證程序的正確性。
時(shí)間序列 --[原理轉(zhuǎn)化]--> 空間關(guān)系
這樣我們就可以使用第三種生產(chǎn)策略:利用構(gòu)造原理進(jìn)行抽象計(jì)算。如果我們只盯著產(chǎn)品的最終形態(tài)看,只是想著怎么把它像搭積木一樣搭建出來(lái),就不可能識(shí)別出
系統(tǒng)結(jié)構(gòu)本身所蘊(yùn)含的對(duì)稱性。如果我們發(fā)現(xiàn)了系統(tǒng)內(nèi)蘊(yùn)的結(jié)構(gòu)特征,但是卻只能通過(guò)構(gòu)造過(guò)程中的行動(dòng)序列來(lái)追隨它,同樣無(wú)法實(shí)現(xiàn)有效的工作復(fù)用。同時(shí)因?yàn)檫@
個(gè)行動(dòng)序列一般處于系統(tǒng)規(guī)則約束之外,完全由人的自覺來(lái)保障,因此很難保證它的正確性。現(xiàn)實(shí)世界的規(guī)范要求并不是模型本身所必須滿足的,只要我們能夠創(chuàng)造
新的結(jié)構(gòu)原理,在概念空間中我們就可以擁有更多的自由。現(xiàn)在業(yè)內(nèi)鼓吹的軟件構(gòu)造原理多半是參照物理世界中生產(chǎn)具體物質(zhì)產(chǎn)品的生產(chǎn)工序,卻沒(méi)有真正把握信息的抽象本質(zhì)。掌握規(guī)則,制訂規(guī)則,才是信息空間中的游戲規(guī)則。
物理學(xué)中最重要的分析學(xué)思想之一是微擾論(Perturbation).
針對(duì)一個(gè)復(fù)雜的物理現(xiàn)象,首先建立一個(gè)全局的規(guī)范的模型,然后考慮各種微擾條件對(duì)原有模型的影響。在小擾動(dòng)情況下,模型的變化部分往往可以被線性化,被局
域化,因而問(wèn)題得到簡(jiǎn)化。微擾分析得到的解依賴于全局模型的解而存在,因而這是一種主從關(guān)系的分解方式。但是如果主體模型是我們已經(jīng)熟知的物理現(xiàn)象,則我
們關(guān)注的重點(diǎn)可以全部放在擾動(dòng)解上,認(rèn)為所有特定的物理規(guī)律都體現(xiàn)在擾動(dòng)解中。如果微擾分析得到的物理元素足夠豐富,則微擾模型本身可以成為獨(dú)立的研究對(duì)
象,在其中我們同樣可以發(fā)現(xiàn)某種普適的結(jié)構(gòu)規(guī)律。
考察如下的構(gòu)造過(guò)程
X = a + b + c
Y = a + b + d = (a + b + c) - c + d = X - c + d
對(duì)于數(shù)學(xué)而言,上述的推導(dǎo)是等價(jià)的,但是對(duì)于物理學(xué)而言,Y = a + b + d 和 Y = X - c +
d是有著本質(zhì)不同的。第一種方式要求打破原先X的構(gòu)造,而重新的組裝其實(shí)是有成本的,特別是在X本身非常復(fù)雜的情況下。典型的,如果X是經(jīng)過(guò)測(cè)試的功能,
重新組裝后原先由測(cè)試保障的概念邊界被打破。
我們可以從Y = X + dX抽象出擾動(dòng)模型 dX = - c + d
主從分解模式自然的導(dǎo)出逆元概念。
如果沒(méi)有逆元,我們必然需要分解。但是如果發(fā)掘了背景這一概念,在逆元運(yùn)算下,對(duì)背景不是分解讓其成為可見的部分,而是采用追加的,增刪的方法對(duì)背景結(jié)構(gòu)
進(jìn)行修正,則我們有可能在沒(méi)有完整背景知識(shí)的情況下,獨(dú)立的理解局部變化的結(jié)構(gòu)。即背景是透明的,知識(shí)成為局部的。在Witrix平臺(tái)中,BizFlow
+ DaoWebAction + StdPage
才構(gòu)成完整的程序模型,BizFlow其實(shí)是對(duì)標(biāo)準(zhǔn)模型的差異描述,但是它可以被單獨(dú)的理解。如果我們從接觸程序開始就接受BizFlow,
就可能完全不需要了解數(shù)據(jù)庫(kù)訪問(wèn)和前臺(tái)界面渲染的知識(shí)。我們并不是通過(guò)在DaoWebAction中設(shè)定各種可預(yù)見的調(diào)用形式,而是在BizFlow中通
過(guò)類似AOP的操作方式直接對(duì)標(biāo)準(zhǔn)模型進(jìn)行修正。這種修正中一個(gè)很重要的部分就是刪除標(biāo)準(zhǔn)模型中缺省提供的功能。
WebMVC之前世今生 http://canonical.javaeye.com/blog/163196
Witrix架構(gòu)分析 http://canonical.javaeye.com/blog/126467
變化的部分構(gòu)成獨(dú)立于原始模型的新的模型,它的結(jié)構(gòu)關(guān)系是完備的,可以獨(dú)立的理解。在原始模型崩潰的情況下,它仍然可能保持有效性。
從物理學(xué)的角度看,我們所觀測(cè)到的一切物理現(xiàn)象,都是某種物理作用的結(jié)果,也就是物質(zhì)結(jié)構(gòu)相對(duì)于背景狀況的一種偏離。我們只可能觀測(cè)到變化的部分,因此我們對(duì)世界的認(rèn)識(shí)其實(shí)只是世界的擾動(dòng)模型而已,世界的本體不屬于科學(xué)研究的范疇。