這兩天終于閑了下來有時間寫點東西了,只記得想寫相機已經是很久遠的事情了,開發(fā)中涉及到相機相關的內容也已經是兩個月之前了。
在3D的世界里相機與矩陣是密不可分的,首先在投影之前,有模型矩陣和視圖矩陣,這兩者并沒有本質上的區(qū)別,一個是站在模型的角度,另一個就是站在觀察者的角度了。模型的左移相當于相機右移,有鑒于此,OPENGL中并不區(qū)分Model Matrix 和 View Matrix,而是將兩者統稱為ModelView Matrix.
以gluLookAt函數為例,該函數根據眼睛的位置,場景中心的位置,以及一個從觀察者視角向上的向量定一個視圖轉換,實際上做的還是應用一個ModelView Matrix。原點位置和眼睛位置確定了z方向向量,向上的向量確定了y方向向量,兩者正交,叉積就是z方向向量了,這樣就可以確定一個視圖矩陣了。
相機不僅僅與ModelView Matrix有關,而且也與投影矩陣有關系。有了相機,再結合ViewPort大小,FOVy(Y方向Field Of View)或者Aspect Ratio,近裁減面,遠裁減面就可以確定透視投影矩陣了。
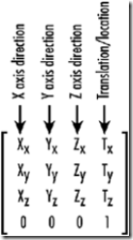
一個4*4的矩陣如何與模型/視圖變換聯系起來呢?看這個圖,前三個列向量分別代表新坐標系的x,y,z軸方向,而最后一個向量則代表平移量(新坐標原點),而矩陣的(4,4)元素則是一個放大因子,他同時將所有點之間的距離放大。如果我們把一個四維向量與之相乘,就可以得到新的坐標了。
什么是萬向節(jié)鎖(Gimbal Lock)呢?這是采用歐拉角的方式表示相機時出現的問題。這個問題源于繞軸旋轉時自由度的丟失。因為旋轉到軸向時將無法確定是從哪個方向旋轉過來的。這就有點像是北極與南極點的經度無法確定一個道理。而且在這個地方,可能出現角度的不連續(xù)變化。即直接從0度跳轉到180度。在相機方向平行于X軸向時,繞X軸的旋轉不會有任何效果,也就是說,從數學上來講此時的ModelView Matrix始終是不變的。在計算時,由于角度變化不連續(xù),所以計算的結果是很不穩(wěn)定的。例如漫游旋轉時,簡單的增加角度,可能在某些臨界值上出現錯誤的情況,典型的就是繞某一個軸的來回震蕩,這也就是所謂Lock的意義了吧。